The area of parallel plates of an air capacitor is 0.2m2 and the distance between them is 0.01m The potential difference between the plates, the potential difference between the plates is 3000V. When a 0.01m thick sheet of an insulating material is placed between the plates, the potential difference decrease to 1000 volt. Determine (i) capacitance of capacitance before placing the sheet (ii) charge on each plate (iii) dielectric constant of material (iv) capacitanc after placing the insulator (v) absoulate permittivity of the dielectric.
The correct Answer is:1.77×10−10F;5.31×10−7C;3;5.31×10−10F;2.66×10−11F.m
To solve the problem step by step, let's break down each part:
Given Data:
- Area of the capacitor plates, A=0.2m2
- Distance between the plates, d=0.01m
- Initial potential difference, V1=3000V
- Potential difference after inserting the dielectric, V2=1000V
(i) Capacitance before placing the sheet
The capacitance C of a parallel plate capacitor is given by the formula:
C=ε0Ad
where:
- ε0=8.85×10−12F/m (permittivity of free space)
Substituting the values:
C=(8.85×10−12F/m)(0.2m2)0.01m
C=1.77×10−120.01
C=1.77×10−10F
(ii) Charge on each plate
The charge Q on the plates can be calculated using the formula:
Q=C×V1
Substituting the values:
Q=(1.77×10−10F)(3000V)
Q=5.31×10−7C
(iii) Dielectric constant of the material
The dielectric constant K can be determined using the relationship between the potential differences before and after inserting the dielectric:
V1V2=K
Substituting the values:
K=3000V1000V=3
(iv) Capacitance after placing the insulator
The capacitance with the dielectric is given by:
C′=K×C
Substituting the values:
C′=3×(1.77×10−10F)
C′=5.31×10−10F
(v) Absolute permittivity of the dielectric
The absolute permittivity ε of the dielectric material can be calculated using:
ε=K×ε0
Substituting the values:
ε=3×(8.85×10−12F/m)
ε=2.655×10−11F/m
Summary of Results:
1. Capacitance before placing the sheet: C=1.77×10−10F
2. Charge on each plate: Q=5.31×10−7C
3. Dielectric constant of material: K=3
4. Capacitance after placing the insulator: C′=5.31×10−10F
5. Absolute permittivity of the dielectric: ε=2.655×10−11F/m
- Area of the capacitor plates, A=0.2m2
- Distance between the plates, d=0.01m
- Initial potential difference, V1=3000V
- Potential difference after inserting the dielectric, V2=1000V
C=ε0Ad
where:
- ε0=8.85×10−12F/m (permittivity of free space)
C=(8.85×10−12F/m)(0.2m2)0.01m
C=1.77×10−120.01
C=1.77×10−10F
Q=C×V1
Substituting the values:
Q=(1.77×10−10F)(3000V)
Q=5.31×10−7C
V1V2=K
Substituting the values:
K=3000V1000V=3
C′=K×C
Substituting the values:
C′=3×(1.77×10−10F)
C′=5.31×10−10F
ε=K×ε0
Substituting the values:
ε=3×(8.85×10−12F/m)
ε=2.655×10−11F/m
1. Capacitance before placing the sheet: C=1.77×10−10F
2. Charge on each plate: Q=5.31×10−7C
3. Dielectric constant of material: K=3
4. Capacitance after placing the insulator: C′=5.31×10−10F
5. Absolute permittivity of the dielectric: ε=2.655×10−11F/m
Topper's Solved these Questions
- ELECTROSTATICSBOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - FILL IN THE BLANKS
8 Videos
- ELECTROSTATICSBOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - PROBLEMS FOR PRACTICE
8 Videos
- ELECTROSTATICSBOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - VALUE BASED QUESTIONS
7 Videos
- ELECTRONIC DEVICESBOOK - PRADEEPCHAPTER - ELECTRONIC DEVICESEXERCISE - Fill in the Blanks
1 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Competition Focus (Multiple Choice Questions)
2 Videos
Similar Questions
The area of parallel plates of an air-filled capacitor is 0.20m2 and the distance between them is 0.01m. The potential difference across the plates is 3000 V. when a 0.01 m thick dielectric sheet is introduced between the plates, then the potential difference decreases to 1000 V. Now, match the two columns (all in SI units).

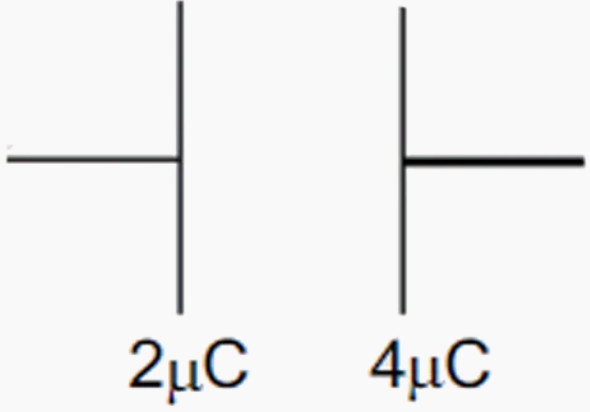
View SolutionIn a parallel plate capacitor of capacitor 1μF two plates are given charges 2μC and 4μC the potential difference between the plates of the capacitor is
View Solution
Knowledge Check
A potential difference between plates of parrallel plate
A3×10−3JB4×10−3JC6×10−3JD5×10−3JDisplacement current is produced between the plates of a capacitor when potential difference between the plates
Ais maximumBis minimumCis zeroDis changing with timeWhen a metal slab is placed between the charged identical , parallel plates , the potential difference between the plates
AdecreasesBincreasesCremains unchanged.Dmay increase or decrease
The force between the plates of a parallel plate capacitor of capacitance C and distance of separation of the plates d with a potential difference V between the plates, is.
View SolutionThe force between the plates of a parallel plate capacitor of capacitance C and distance of separation of the plates d with a potential difference V between the plates, is.
View SolutionWhen potential difference of 9V is applied between the two plates, electron accelerate between the plates with velocity
View SolutionIn an isolated parallel plate capacitor of capacitance C, the plates have charge Q1 and Q2. The potential difference between the plates is
View SolutionA parallel plate air capacitor has capacity C distance of separation between plates is d and potential difference V is applied between the plates force of attraction between the plates of the parallel plate air capacitor is
View Solution
