The two plates of a parallel plate capacitor are 4mm apart. A slab of dielectric constant 3 and thickness 3mm is introduced between the plates is so adujected that the capacitance of the capacitor becomes 23rd of its original value. What is the new distance between the plates ?
The correct Answer is:8mm
To solve the problem, we will follow these steps:
Step 1: Understand the original capacitance
The capacitance C of a parallel plate capacitor is given by the formula:
C=ε0AD
where:
- ε0 is the permittivity of free space,
- A is the area of the plates,
- D is the distance between the plates.
Given that the original distance D=4mm.
Step 2: Introduce the dielectric slab
When a dielectric slab of thickness T=3mm and dielectric constant K=3 is introduced, the new capacitance C′ can be calculated using the formula:
C′=ε0AD′−T+ε0AT/K
where D′ is the new distance between the plates after adjustment.
Step 3: Set up the equation for the new capacitance
According to the problem, the new capacitance C′ is 23 of the original capacitance C:
C′=23C
Substituting the expression for capacitance, we have:
ε0AD′−T+ε0AT/K=23⋅ε0AD
Step 4: Substitute known values
Substituting D=4mm, T=3mm, and K=3:
ε0AD′−3+ε0A3/3=23⋅ε0A4
This simplifies to:
1D′−3+1=212
which simplifies to:
1D′−3+1=16
Step 5: Solve for D′
Rearranging the equation:
1D′−3=16−1
1D′−3=1−66=−56
Taking the reciprocal gives:
D′−3=−65
Thus:
D′=3−65=155−65=95=1.8mm
Step 6: Convert to mm
Since we need the final answer in mm, we convert:
D′=1.8mm
Final Answer
The new distance between the plates is:
D′=1.8mm
The capacitance C of a parallel plate capacitor is given by the formula:
C=ε0AD
where:
- ε0 is the permittivity of free space,
- A is the area of the plates,
- D is the distance between the plates.
When a dielectric slab of thickness T=3mm and dielectric constant K=3 is introduced, the new capacitance C′ can be calculated using the formula:
C′=ε0AD′−T+ε0AT/K
where D′ is the new distance between the plates after adjustment.
According to the problem, the new capacitance C′ is 23 of the original capacitance C:
C′=23C
ε0AD′−T+ε0AT/K=23⋅ε0AD
Substituting D=4mm, T=3mm, and K=3:
ε0AD′−3+ε0A3/3=23⋅ε0A4
1D′−3+1=212
which simplifies to:
1D′−3+1=16
Rearranging the equation:
1D′−3=16−1
1D′−3=1−66=−56
Taking the reciprocal gives:
D′−3=−65
Thus:
D′=3−65=155−65=95=1.8mm
Since we need the final answer in mm, we convert:
D′=1.8mm
The new distance between the plates is:
D′=1.8mm
Topper's Solved these Questions
- ELECTROSTATICSBOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - FILL IN THE BLANKS
8 Videos
- ELECTROSTATICSBOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - PROBLEMS FOR PRACTICE
8 Videos
- ELECTROSTATICSBOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - VALUE BASED QUESTIONS
7 Videos
- ELECTRONIC DEVICESBOOK - PRADEEPCHAPTER - ELECTRONIC DEVICESEXERCISE - Fill in the Blanks
1 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Competition Focus (Multiple Choice Questions)
2 Videos
Similar Questions
The two plates of a parallel plate capacitor are 4 mm apart . A slab of dielectric constant 3 and thickness 3 mm is introduced between the plates with its face parallel to them . The distance between the plates is so adjusted that the capacity of the capacitor becomes 23 rd of its original value . What is the new distance the plates ?
View SolutionThe distance between the plates of a parallel plate capacitor is 'd'. The capacitance of the capacitor gets doubled when a metal plate of thicknessd2 is placed between the plates.
View Solution
Knowledge Check
A parallel plate capacitor has a capacity c. If a medium of dielectric constant K is introduced between plates, the capacity of capacitor becomes
ACKBCK2CK2CDKCSeparation between the plates of a parallel plate capacitor is d and the area of each plates is A. When a slab of material of dielectric constant k and thickness t(t<d) is introduced between the plates. Its capacitance becomes
Aε0Ad+t(1−1k)Bε0Ad+t(1+1k)Cε0Ad−t(1−1k)Dε0Ad−t(1+1k)The plates of a parallel plate capacitor with air as medium are separated by a distance of 8mm. A medium of dielectric constant 2 and thickness 4mm having the same area is introduced between the plates. For the capacitanace to remain the same, the distance between the plates is
A8mmB6mmC10mmD12mm
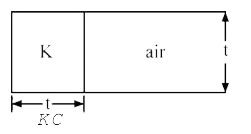
A parallel plate capacitor with air as the dielectric has capacitance C. A slab of dielectric constant K and having the same thickness as the separation between plates is introduced so as to fill one-fourth of the capacitor as shown in the figure. The new capacitance will be :
View SolutionA parallel plate capacitor carries a harge Q. If a dielectric slab with dielectric constant K=2 is dipped between the plates, then
View SolutionA parallel -plate air capacitor has capacity C. A dielectric slab of dielectric constant K, whose thickness is half of the air gap between the plates, is now inserted between the plates. The capacity of the capacitor will now be
View SolutionThe separation between the plates of a parallel plate capacitor is d and the area of each plate is A. iff a dielectric slab of thickness x and dielectric constant K is introduced between the plates, then the capacitance will be
View SolutionThe distance between the plates of a parallel plate condenser is 8mm and P.D.120 volts. If a 6mm thick slab of dielectric constant 6 is introduced between its plates, then
View Solution
