Two capacitors of and are joined in series. The outer plate of second capacitor is earthed. Find out the potential and charge of the inner plate of each capacitor.
The correct Answer is:
To solve the problem of finding the potential and charge of the inner plates of two capacitors connected in series, we can follow these steps:
Step 1: Identify the Capacitors and Their Values
We have two capacitors:
- Capacitor 1 (C1) = 2 µF
- Capacitor 2 (C2) = 3 µF
Step 2: Determine the Configuration
The capacitors are connected in series, and the outer plate of the second capacitor is earthed (i.e., it is at 0 volts).
Step 3: Calculate the Equivalent Capacitance
The formula for the equivalent capacitance (C_eq) of capacitors in series is given by:
1Ceq=1C1+1C2
Substituting the values:
1Ceq=12+13=3+26=56
Thus,
Ceq=65μF=1.2μF
Step 4: Calculate the Total Charge (Q)
The total charge (Q) in the series circuit can be calculated using the formula:
Q=Ceq×V
Where V is the total potential difference across the series combination. Since the outer plate of the first capacitor is at 1000 volts and the outer plate of the second capacitor is earthed (0 volts), the total potential difference is:
V=1000V−0V=1000V
Now substituting the values:
Q=1.2μF×1000V=1200μC
Step 5: Calculate the Potential Difference Across Each Capacitor
1. For Capacitor 1 (C1):
The potential difference (V1) across the first capacitor can be calculated using:
V1=QC1=1200μC2μF=600V
2. For Capacitor 2 (C2):
The potential difference (V2) across the second capacitor can be calculated using:
V2=QC2=1200μC3μF=400V
Step 6: Determine the Potentials of the Inner Plates
- The potential of the inner plate of Capacitor 1 (V1) is:
Vinner1=1000V−V1=1000V−600V=400V
- The potential of the inner plate of Capacitor 2 (V2) is:
Vinner2=0V+V2=0V+400V=400V
Final Results
- Charge on both capacitors: Q=1200μC
- Potential of the inner plate of Capacitor 1: 400V
- Potential of the inner plate of Capacitor 2: 400V
We have two capacitors:
- Capacitor 1 (C1) = 2 µF
- Capacitor 2 (C2) = 3 µF
The capacitors are connected in series, and the outer plate of the second capacitor is earthed (i.e., it is at 0 volts).
The formula for the equivalent capacitance (C_eq) of capacitors in series is given by:
1Ceq=1C1+1C2
Substituting the values:
1Ceq=12+13=3+26=56
Thus,
Ceq=65μF=1.2μF
The total charge (Q) in the series circuit can be calculated using the formula:
Q=Ceq×V
Where V is the total potential difference across the series combination. Since the outer plate of the first capacitor is at 1000 volts and the outer plate of the second capacitor is earthed (0 volts), the total potential difference is:
V=1000V−0V=1000V
Now substituting the values:
Q=1.2μF×1000V=1200μC
1. For Capacitor 1 (C1):
The potential difference (V1) across the first capacitor can be calculated using:
V1=QC1=1200μC2μF=600V
The potential difference (V2) across the second capacitor can be calculated using:
V2=QC2=1200μC3μF=400V
- The potential of the inner plate of Capacitor 1 (V1) is:
Vinner1=1000V−V1=1000V−600V=400V
- The potential of the inner plate of Capacitor 2 (V2) is:
Vinner2=0V+V2=0V+400V=400V
- Charge on both capacitors: Q=1200μC
- Potential of the inner plate of Capacitor 1: 400V
- Potential of the inner plate of Capacitor 2: 400V
Topper's Solved these Questions
- ELECTROSTATICSBook:PRADEEPChapter:ELECTROSTATICSExercise:FILL IN THE BLANKS
Explore 8 Videos
- ELECTROSTATICSBook:PRADEEPChapter:ELECTROSTATICSExercise:PROBLEMS FOR PRACTICE
Explore 8 Videos
- ELECTROSTATICSBook:PRADEEPChapter:ELECTROSTATICSExercise:VALUE BASED QUESTIONS
Explore 7 Videos
- ELECTRONIC DEVICESBook:PRADEEPChapter:ELECTRONIC DEVICESExercise:Fill in the Blanks
Explore 1 Video
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:PRADEEPChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Competition Focus (Multiple Choice Questions)
Explore 2 Videos
Similar Questions
A capacitor of 20μF is charged to a potential of 10kV. Find th charge accumulated on each plate of the capacitor.
View SolutionTwo capacitors of capacitances 3μFand6μF, are charged to potentials 2V and 5V respectively. These two charged capacitors are connected in series. Find the potential across each of the two capacitors now.
View Solution
Knowledge Check
Two capacitors of capacitance 2μF and 3μF are joined in series. Outer plate first capacitor is at 1000 volt and outer plate of second capacitor is earthed (grounded). Now the potential on inner plate of each capacitor will be
A700 VoltB200 VoltC600 VoltD400 VoltTwo capacitors of 2μF and 3μF are connected in series. The potential at point A is 1000 volt and the outer plate of 3μF capacitor is earthed. The potential at point B is
 A300 voltB500 voltC600 voltD400 volt
A300 voltB500 voltC600 voltD400 voltThree capacitors of 2μF,3μFand6μF are joined in series and the combination is charged by means of a 24 V battery. The potential difference between the plates of the 6μF capacitor is
A4VB6 VC8VD10 V
Three capacitors 1, 2 and 4μ f are connected in series to a 10 volt source.The charge on the plate of middle capacitor is....
View SolutionThree capcaitors of capacities 1μF,2μF and 3μF are charged by 10V,20V and 30V respectively. Now positive plates of first two capacitors are connected with the negative plate of third capacitor on one side and negative plates of first wo capacitors are connectes with positive of third capacitor on the other side. Find
a. common potential V
b. final charges on different capacitors.
View SolutionThree capacitors of 2μF,3μF and 6μF are joined in series and the combination is charged by means of a 24 volt battery. The potential difference between the plates of the 6μF capacitor is
View SolutionThe capacitor of capacitance 4μF and 6μF are connected in series. A potential difference of 500 volts applied to the outer plates of the two capacitor system. Then the charge on each capacitor is numerically
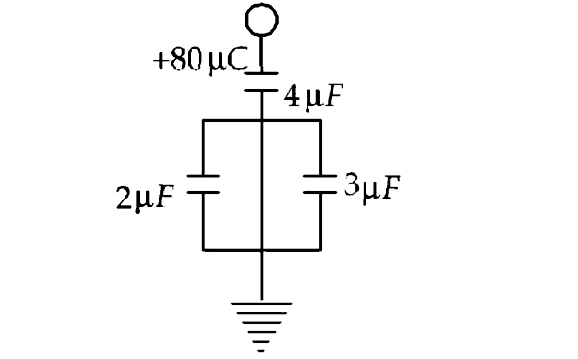
View SolutionIn the given circuit, a charge of +80μC is given to the upper plate of the 4μF capacitor. Then in the steady state, the charge on the upper plate of the 3μF capacitor is
View Solution

