A plank with a small block on top of it is under going vertical SHM. Its period is 2sec. The minium amplitude at which the block will separate from plank is :
10π2
π210
20π2
π10
The correct Answer is:A
To solve the problem of determining the minimum amplitude at which a block will separate from a plank undergoing vertical simple harmonic motion (SHM), we can follow these steps:
1. Understanding the Problem:
- We have a plank with a small block on top of it, and the plank is undergoing vertical SHM.
- The time period (T) of the SHM is given as 2 seconds.
- We need to find the minimum amplitude (A) at which the block will separate from the plank.
2. Condition for Separation:
- The block will separate from the plank when the upward acceleration of the plank exceeds the acceleration due to gravity (g).
- This means that the maximum acceleration (a_max) of the plank must be greater than or equal to g.
3. Maximum Acceleration in SHM:
- The maximum acceleration (a_max) in SHM can be expressed as:
amax=Aω2
- Where:
- A = amplitude
- ω = angular frequency
4. Finding Angular Frequency (ω):
- The angular frequency (ω) is related to the time period (T) by the formula:
ω=2πT
- Substituting T = 2 seconds:
ω=2π2=πrad/s
5. Setting Up the Inequality:
- For the block to just separate from the plank, we set up the inequality:
Aω2≥g
- Substituting ω:
Aπ2≥g
6. Solving for Amplitude (A):
- Rearranging the inequality gives:
A≥gπ2
7. Substituting Values:
- Using g = 9.8 m/s²:
A≥9.8π2
- Calculating π²:
π2≈9.87
- Therefore:
A≥9.89.87≈0.9927m
8. Converting to Centimeters:
- To express this in centimeters:
A≥0.9927×100≈99.27cm
Final Answer:
The minimum amplitude at which the block will separate from the plank is approximately 99.27 cm.
---
- We have a plank with a small block on top of it, and the plank is undergoing vertical SHM.
- The time period (T) of the SHM is given as 2 seconds.
- We need to find the minimum amplitude (A) at which the block will separate from the plank.
- The block will separate from the plank when the upward acceleration of the plank exceeds the acceleration due to gravity (g).
- This means that the maximum acceleration (a_max) of the plank must be greater than or equal to g.
- The maximum acceleration (a_max) in SHM can be expressed as:
amax=Aω2
- Where:
- A = amplitude
- ω = angular frequency
- The angular frequency (ω) is related to the time period (T) by the formula:
ω=2πT
- Substituting T = 2 seconds:
ω=2π2=πrad/s
- For the block to just separate from the plank, we set up the inequality:
Aω2≥g
- Substituting ω:
Aπ2≥g
- Rearranging the inequality gives:
A≥gπ2
- Using g = 9.8 m/s²:
A≥9.8π2
- Calculating π²:
π2≈9.87
- Therefore:
A≥9.89.87≈0.9927m
- To express this in centimeters:
A≥0.9927×100≈99.27cm
The minimum amplitude at which the block will separate from the plank is approximately 99.27 cm.
Similar Questions
A block is kept on a rough horizontal plank. The coefficient of friction between block and plank is 1/2. Plank is undergoing SHM is angular frequency 10rad/s. Find the maximum amplitude of plank in which the block does slip over plank (g=10m/s2).
View SolutionA block is resting on a piston which is moving vertically with simple harmonic motion of period 1.0 second. At what amplitude of motion will the block and piston separate? What is the maximum velocity of the piston at this amplitude?
View Solution
Knowledge Check
A block of mass m is resting on a piston as shown in figure which is moving vertically with a SHM of period 1s. The minimum amplitude of motion at which the block and piston separate is :
 A0.25mB0.52mC2.5mD0.15m
A0.25mB0.52mC2.5mD0.15mA block of mass ‘m’ rests on a piston executing S.H.M. of period 1sec. The amplitude of oscillations so that the mass is separated from the piston is
A0.25 mB0.5 mC1mDzeroA small block of mass 1kg is placed over a plank of mass 2kg. The length of the plank is 2 m. coefficient of friction between the block and the plnak is 0.5 and the ground over which plank in placed is smooth. A constant force F=30N is applied on the plank in horizontal direction. the time after which the block will separte from the plank is (g=10m/s2)
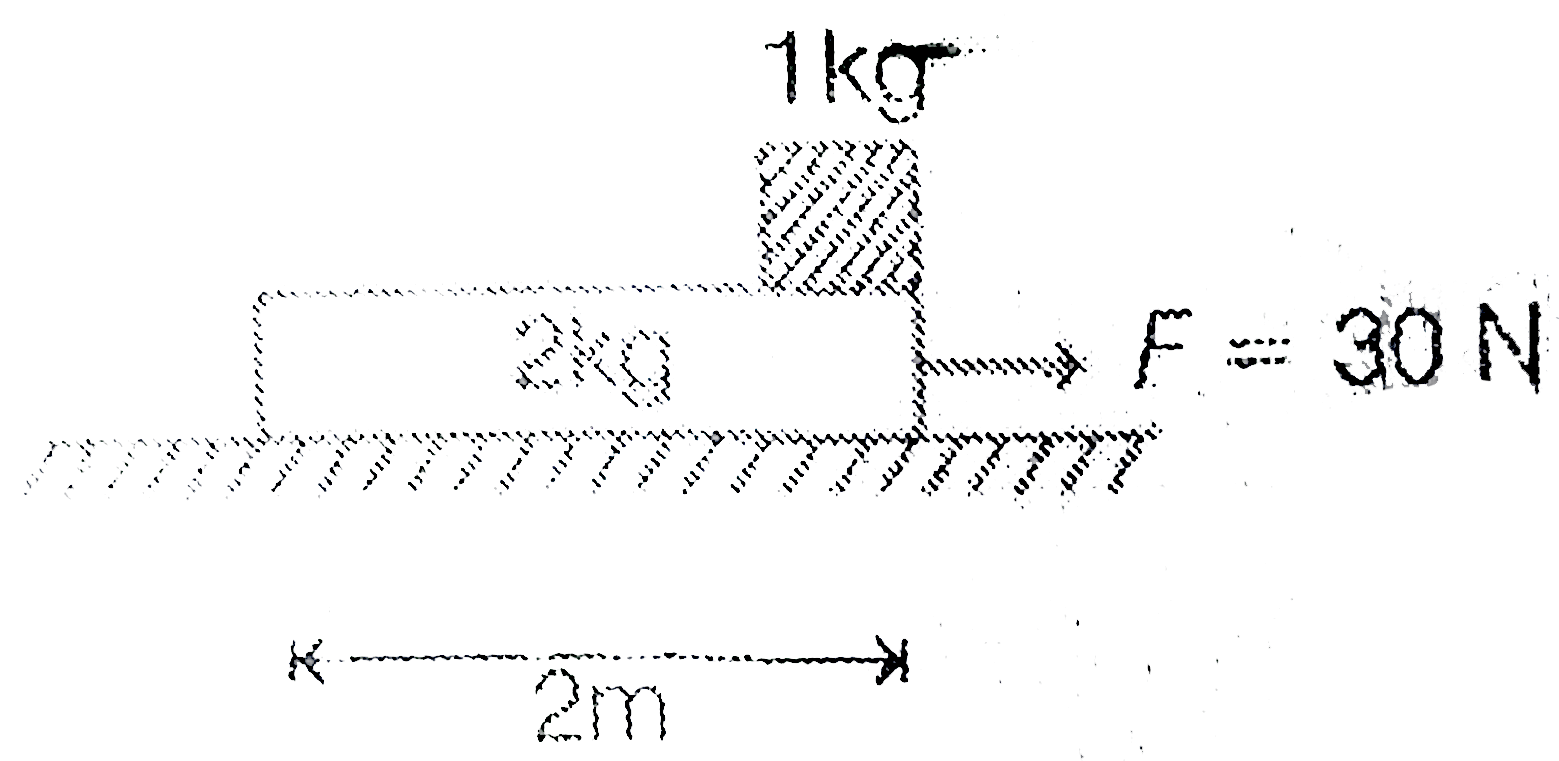 A0.89sB1.2sC0.62sD1.6s
A0.89sB1.2sC0.62sD1.6s
A block is resting on a piston which is moving vertically with simple harmonic motion of period 1.0 second. At what amplitude of motion will the block and pisto separate? What is the maximum velocity of the piston at this amplitude?
View SolutionA block is kept on a rough horizontal plank. The coefficient of friction between the block and the plank is 12. The plank is undergoing SHM of angular frequency 10 rad/s. The maximum amplitude of plank in which the block does not slip over the plank is (g= 10 m/s2)
View SolutionA block is resting on a piston which executes simple harmonic motion in vertical plain with a period of 2.0s in vertical plane at an amplitude just sufficient for the block to separate from the piston. The maximum velocity of the piston is
View SolutionA horizontal platform with a small block of mass 1 kg kept on it performs vertical SHM of amplitude 1 cm. The block does not lose contact with the platform anywhere. The minimum possible time period of the platform
View SolutionA horizontal plank has a rectangular block placed on it. The plank starts oscillating vertically and simple harmonically with an amplitude of 40 cm. The block just loses contact with the plank when the latter is at momentary rest Then.
View Solution

