A clock is performing SHM along a vertical line with amplitude of 40 cm on a horizontal plank. The block just lose the contact with plank when plank is momentarily at rest. Then, (Take, g=10m/s2)
the period of its oscillation is 2π5s
the period of is oscillation is 2π6s
the period of its oscillation is π5s
None of the above
The correct Answer is:A
The block just loose the contact from the plank if acceleration of plank just equal to g. (Vertiaclly downward)
Since, block just loses contact, when the plank is momentarily at rest. Therefore, at that instant the plank is at its upper extreme postion.
But at extreme position acceleration =aω2
where, a = 40 cm = 0.4m
Hence, 0.4ω2=g=10m/s2
ω=5rad/s ⇒ T=2π5s
Topper's Solved these Questions
Similar Questions
An object kept on the platform a horizontal platform executing SHM, up and down with amplitude 80 cm. At what frequency will the object just lose contact with the platform?
View SolutionA plank with a bar placed on it performs horizontal harmonic oscillations with amplitude a=10cm. Find the coefficient of friction between the bar and the plank if the former starts sliding along the plank when the amplitude of oscillation of the plank becomes less than T=1.0s.
View Solution
Knowledge Check
A horizontal plank has a rectangular block placed on it. The plank starts oscillating vertically and simple harmonically with an amplitude of 40 cm. The block just loses contact with the plank when the latter is at momentary rest Then.
Athe period of oscillation is (2π5)Bthe block weighs double its actual weght, then the plank is at one of the positions of momentary rest.Cthe block weighs 1.5 times its weight on the plank halfway downDthe block weghs its true weight on the plank when the later moves fastest.A horizontal platform with an object placed on it is executing S.H.M. in the vertical direction. The amplitude of oscillation is 2.5 cm. If the object is not detached from the platform, then the least period of these oscillations will be, (g=10m/s2)
A0.1πsBπsC0.5πsD2πsA block of mass 2 kg rests on a rough horizontal plank , the coefficient of friction between the plank and block is 0.3. If the plank is pulled horizontally with a constant acceleration of 4m/s2 , the distance moved by the block on the plank in 5 second starting from rest (in m) is : (Take g = 10m/s2)
A5B10C25D50
A huge piston in a machine is undergoing, vertical S.H.M approximately with a frequency of 1 s−1. A 5 kg block is placed on the piston. iF the block and the piston move together, determine the maximum amplitude of the piston S.H.M. such that block remains in contact with piston
take, g = 9.8 m/s2
View SolutionA horizontal platform with a small block of mass 1 kg kept on it performs vertical SHM of amplitude 1 cm. The block does not lose contact with the platform anywhere. The minimum possible time period of the platform
View SolutionA book is resting on shelf that is undergoing vertical simple harmonic oscillations with an amplitude of 2.5 cm. What is the minimum frequency of oscillation of the shell for which the book will lose contact with the shelf ? (Assume that g=10m/s2)
View SolutionA block of mass m =2 kg is placed on a plank of mass M = 10 kg, which is placed on a smooth horizontal plane as shown in the figure. The coefficient of friction between the block and the plank is μ=13. If a horizontal force F is applied on the plank, then the maximum value of F for which the block and the plank move together is (g=10m/s2)
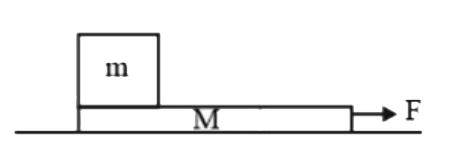
View SolutionA block is kept on a rough horizontal plank. The coefficient of friction between the block and the plank is 12. The plank is undergoing SHM of angular frequency 10 rad/s. The maximum amplitude of plank in which the block does not slip over the plank is (g= 10 m/s2)
View Solution
