What is the maximum acceleration of the particle doing the SHM γ=2sin[πt2ϕ] where gamma is in cm?
π2cm/s2
π22cm/s2
π4cm/s2
π4cm/s2
The correct Answer is:B
y=2sin(πt2+ϕ)
Comparing the equation with the standard equation
y=Asin(ωt+ϕ)
So A=2cm,ω=π2
Acceleration of particle is
a=ω2x [numerically]
At x=+A,a=amax<br>therefore" "a_("max")=omega^(2)A=((pi)/(2))^(2)xx2<br>=2xx(pi^(2))/(4)=(pi^(2))/(2)cm//s^(2)
Topper's Solved these Questions
Similar Questions
The velocity time graph of a particle executing SHM is shown. The maximum acceleration of the particle is nπm/s2, where n is______.
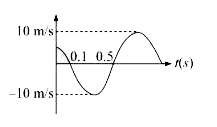
View SolutionDerive an expression for the instantaneous acceleration of a particle executing S.H.M. Find the position where acceleration is maximum and where it is minimum.
View Solution
Knowledge Check
What is the maximum acceleration of the particle doing the SHM? y=2sin[πt2+ϕ], where y is in cm
Aπ2cm/s2Bπ22cm/s2Cπ4cm/s2Dπ24cm/s2If y = 2 (cm) sin[πt2+ϕ] then the maximum acceleration of the particle doing the S.H.M. is
Aπ2 cm/s2Bπ22 cm/s2Cπ24 cm/s2Dπ4 cm/s2The maximum velocity and maximum acceleration of a particle executing SHM are 20 cm s−1and100cms−2. The displacement of the particle from the mean position when its speed is 10 cm s−1 is
A2 cmB2.5 cmC2√3cmD2√2cm
The diameter of the reference circle for a particle performing linear SHM is 10 cm. If the reference particle performs UCM with period 2π seconds, what is the maximum acceleration of the particle in linear SHM ?
View SolutionMaximum acceleration of a particle in SHM is 16cm/s2 and maximum uelocity is 8cm/s.Find time period and amplitude of oscillations.
View SolutionThe displacement of a particle of mass 1 kg in S.H.M. is x = 2 sin (πt+ϕ)m. Then variation of its PE in joule is
View SolutionThe equation for the displacement of a particle executing SHM is x=5sin(2πt)cm Then the velocity at 3cm from the mean position is( in cm//s)
View SolutionAmongst α,β and γ−particles, α−particle has maximum penetrating power.
The α−particle is heavier than β and γ−particle.
View Solution