Figure shows a vertical force applied tangentially to a uniform cylinder of weight Fg. The coefficient static friction between the cylinder and both surface is 0.500. In terms of Fg, find the maximum force P that can be applied that does not cause the cylinder to rotate.
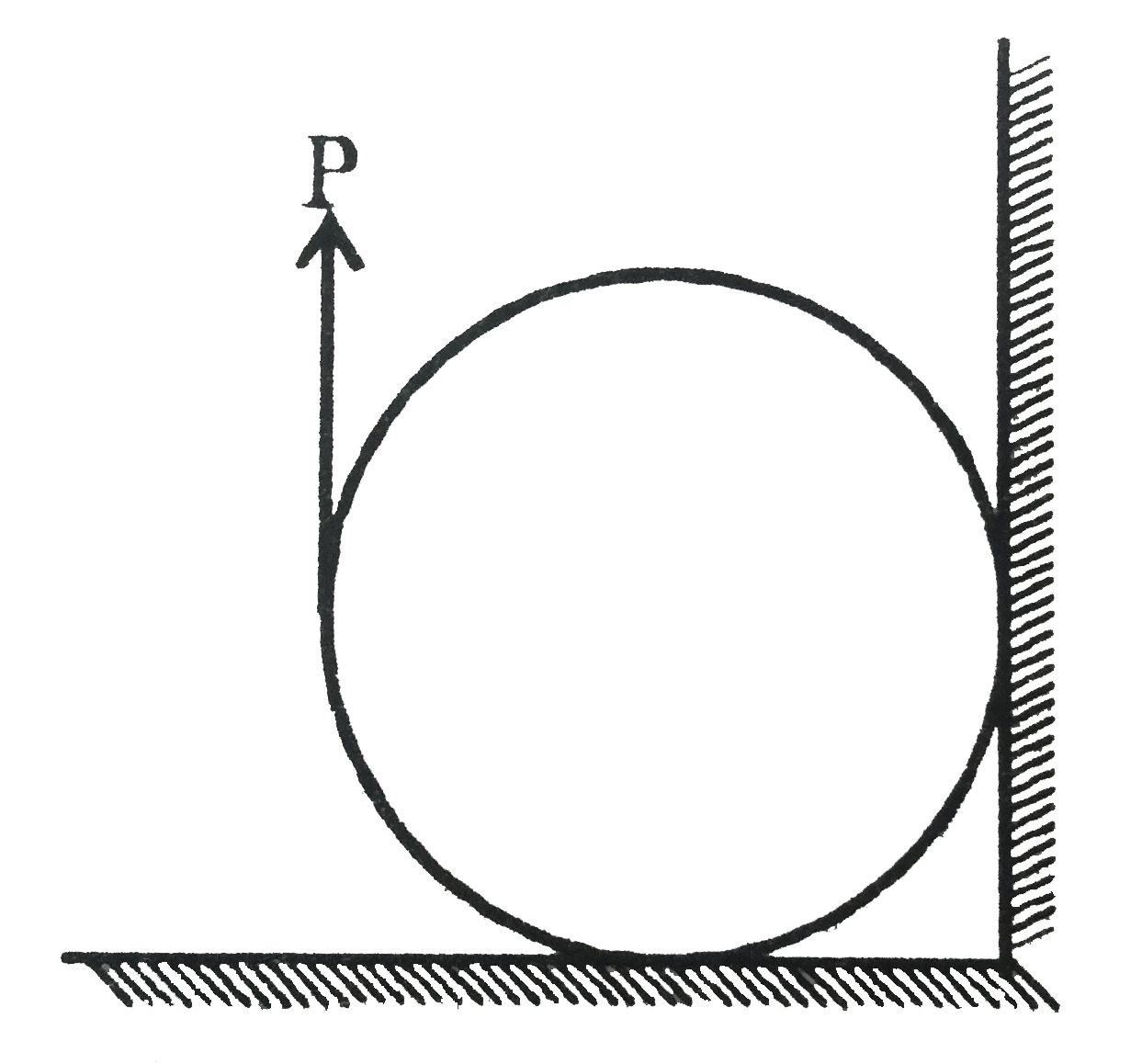 .
.
The correct Answer is:38Fg
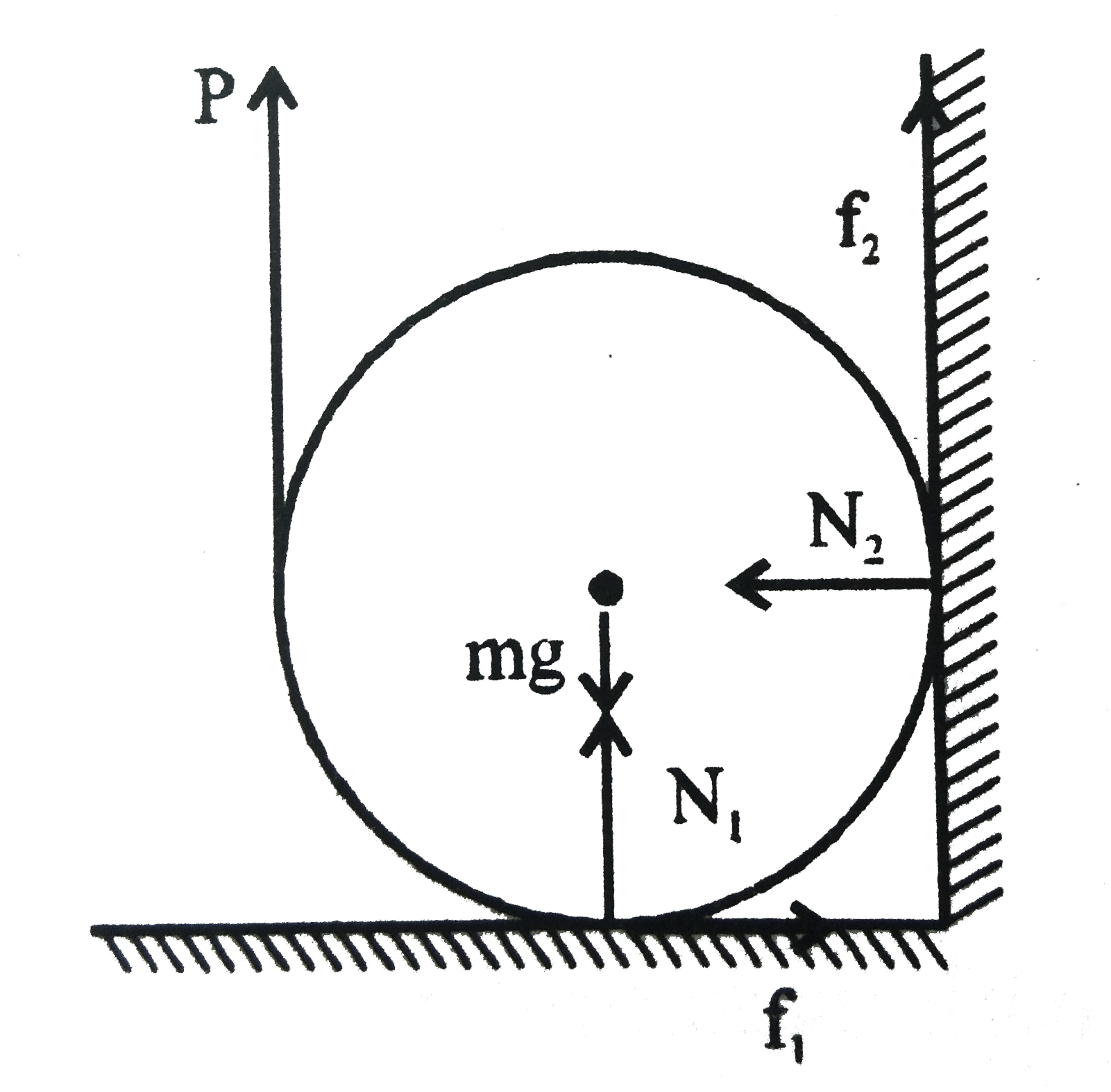
Wt=Fg
μ=0.5
The cylinder is in both translational and rotational equilibrium.
:. Force is balance
P+f2+N1=Fg …(1)
N2=f1 ….(2)
Torque is also balance about COM
f1×R+f2×R−P×R=0
f1+f2=P
as force is maximum
μN1+μN2=P
μ(N1+N2)=P
From (2)
μ(N1+μN1)=P or N1=Pμ(1+μ)....(3)
from (1) and (2) P+μN2+N1=Fg
P+μ×μN1+N1=Fg
(μ2+1)N1=Fg−P ....(4)
from (3) and (4) Pμ(1+μ)=Fg−P(μ2+1)
Put μ=0.5, we gate P=38Fg.
Similar Questions
Figure shows a vertical force applied tangentially to a uniform cylinder of weight Fg. The coefficient of static friction between the cylinder and all surfaces is 0.500. In terms of Fg , find the maximum force P that can be applied that does not cause the cylinder to rotate.

View SolutionConsider the situation shown in the figure . The coefficient of friction between the blocks is μ. Find the minimum and the maximum force F that can be applied so that two blocks move together.

View Solution
Knowledge Check
A uniform cylinder rests on a cart as shown. The coefficient of static friction between the cylinder and the cart is 0.5 If the cylinder is 4cm in diameter and 10cm in height, which of the following is the minimum acceleration of the cart needed to cause the cylinder to tip over ?
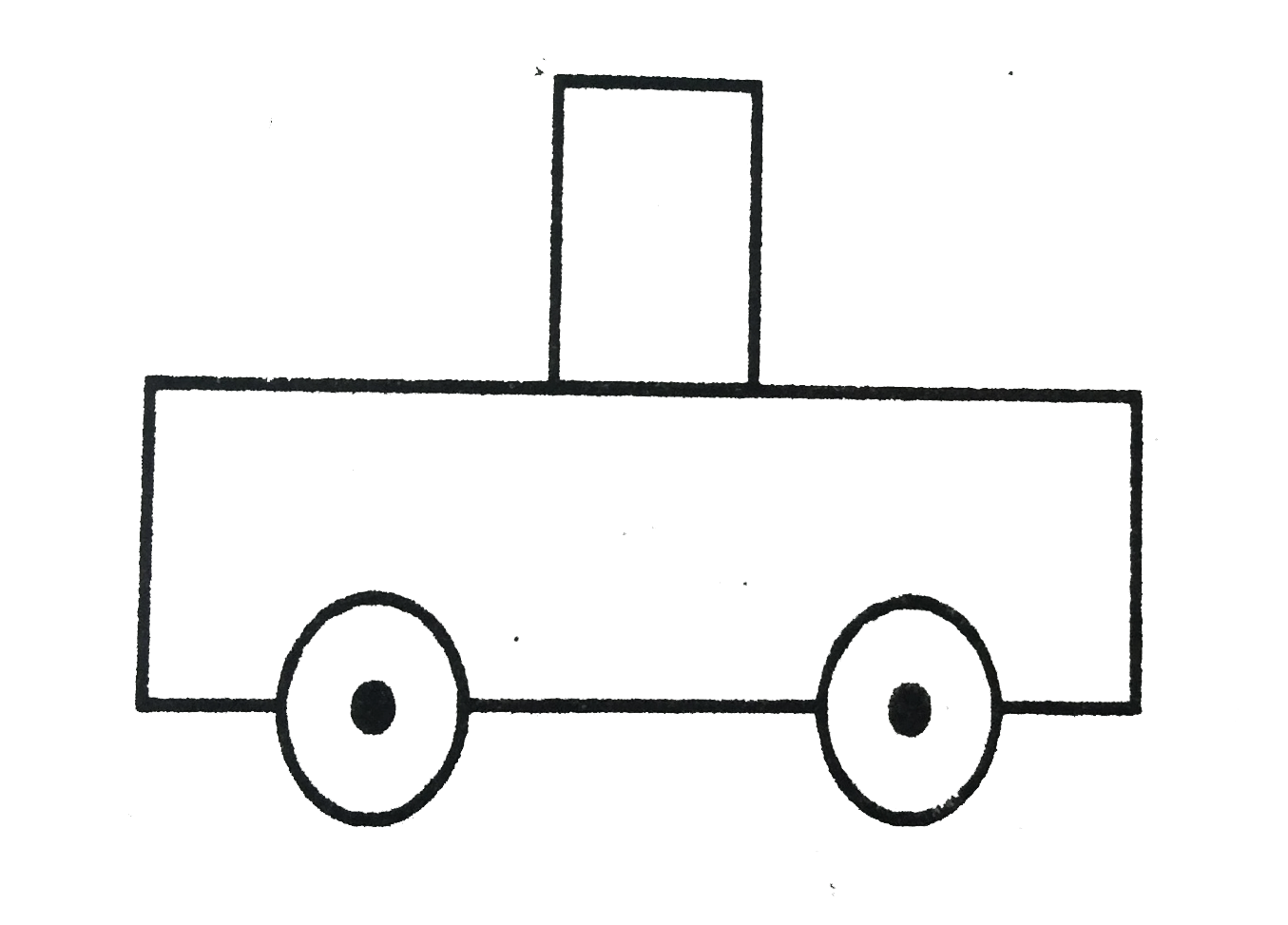 .A2m/s2B4m/s2C5m/s2Dthe cylinder would slide before it before it begins to tip over.
.A2m/s2B4m/s2C5m/s2Dthe cylinder would slide before it before it begins to tip over.If the coefficient of friction between all surface figure is 0.4 then find the minimum force F to have equilibrium of the system.
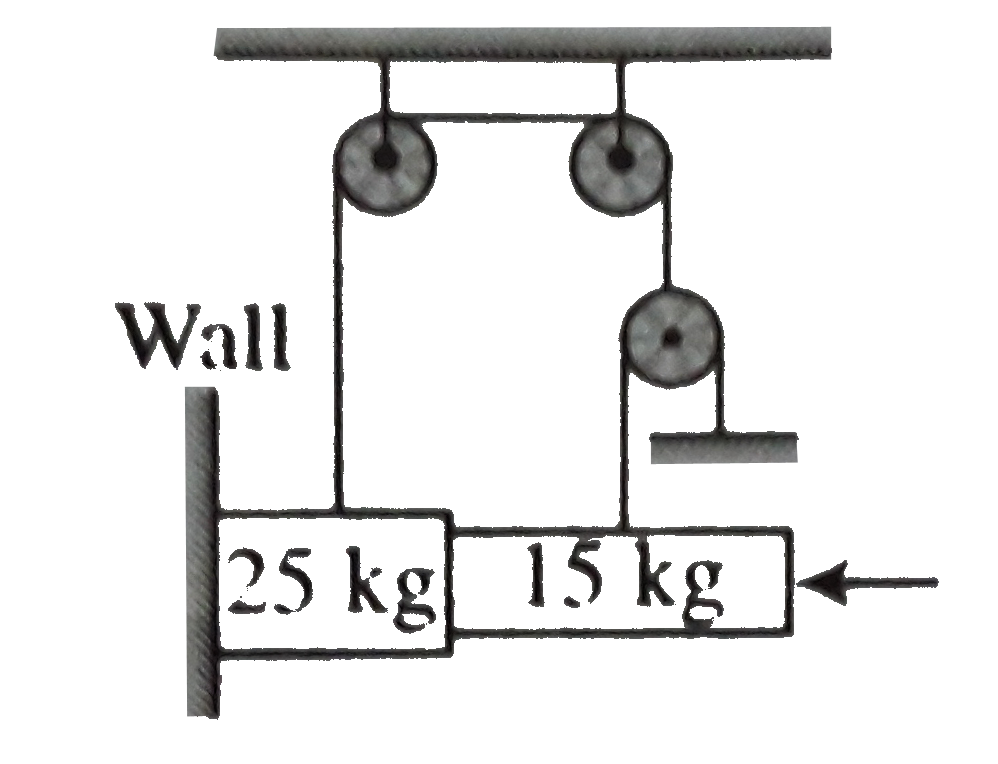 A62.5NB150NC31.25ND50N
A62.5NB150NC31.25ND50N
The coefficient of static friction between two blocks is 0.5 and the table is smooth. The maximum horizontal force that can be applied to move the blocks together is N. (take g=10ms−2)

View SolutionA ring of mass M is kept on w horizontal rough surface . A force F is applied tangentially at its rim as shown . The coefficient of friction between the ring and surface is μ Then

View SolutionThe coefficient of static friction between the two blocks shown in figure is μ and the table is smooth. What maximum horizontal forced F can be applied to he block of mass M so that the block move together?

View SolutionA cylinder of mass 10kg is rolling perfectly on a plane of inclination 30∘. Find the force of friction between the cylinder and the surface of inclined plane.
View SolutionA solid cylinder of mass 10 kg is rolling perfectly on a plane of inclination 30∘. Find the force of friction between the cylinder and the surface of the inclined plane.
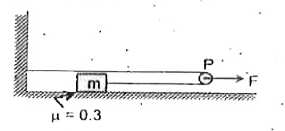
View SolutionA block of mass m = 2kg is accelerating by a force F = 20N applied on a smooth light pulley as shown in the figure. If the coefficient of kinetic friction between the block and the surface is μ=0.3, find its acceleration.
View Solution

