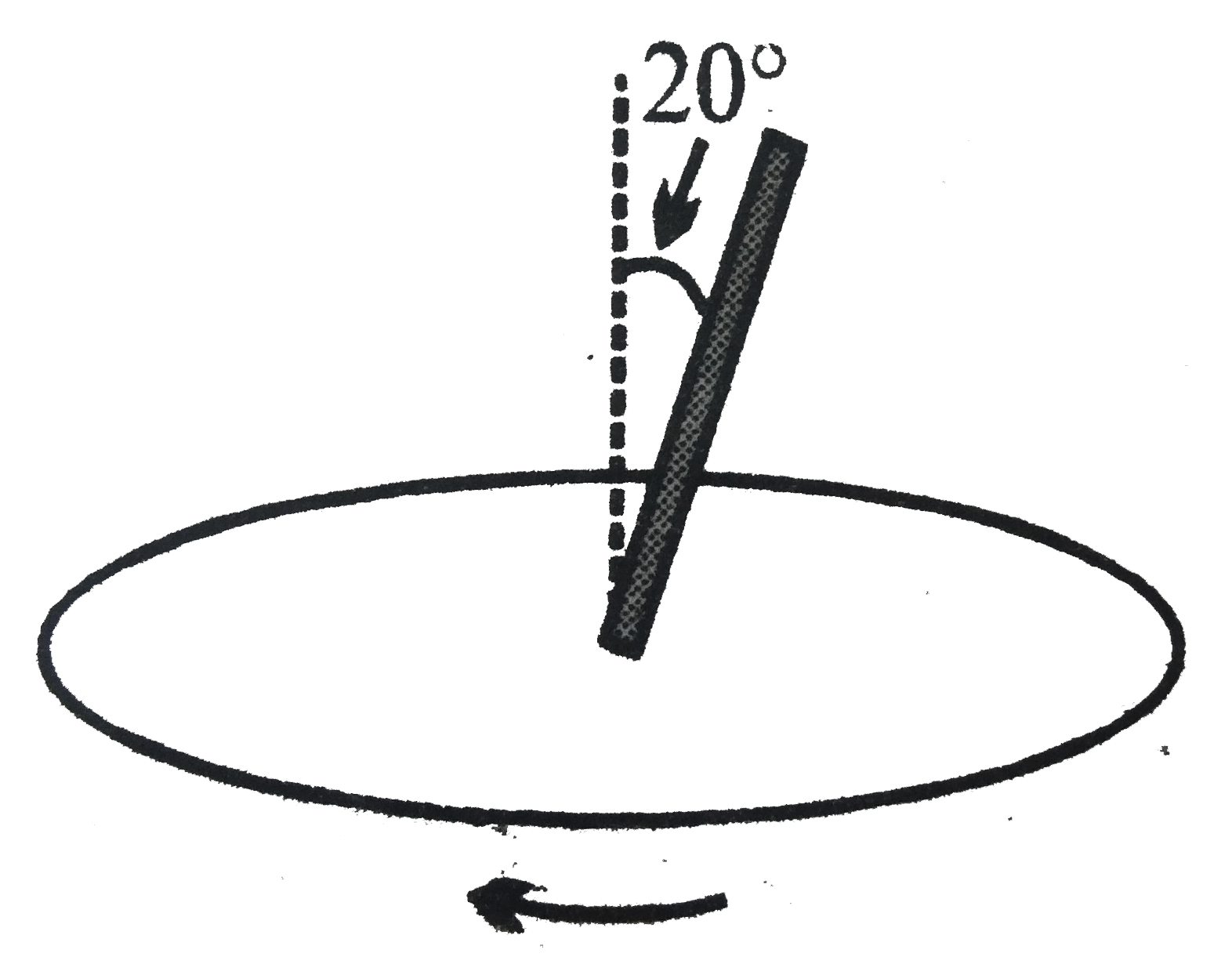
A uniform rod is fixed to a rotating turntable so that its lower end is on the axis of the turntable and it makes an angle of 20% to the vertical. (The rod is thus rotating with uniform angular velocity about a vertical axis passing through one end.) If the turntable is rotating clockwise as seen from above.
 .
.
What is the direction of the rod's angular momentum vector (calculated about its lower end) ?
vertically downwards
down at 20∘ to the horizontal
up at 20∘ to the horizontal
vertically upwards
The correct Answer is:B
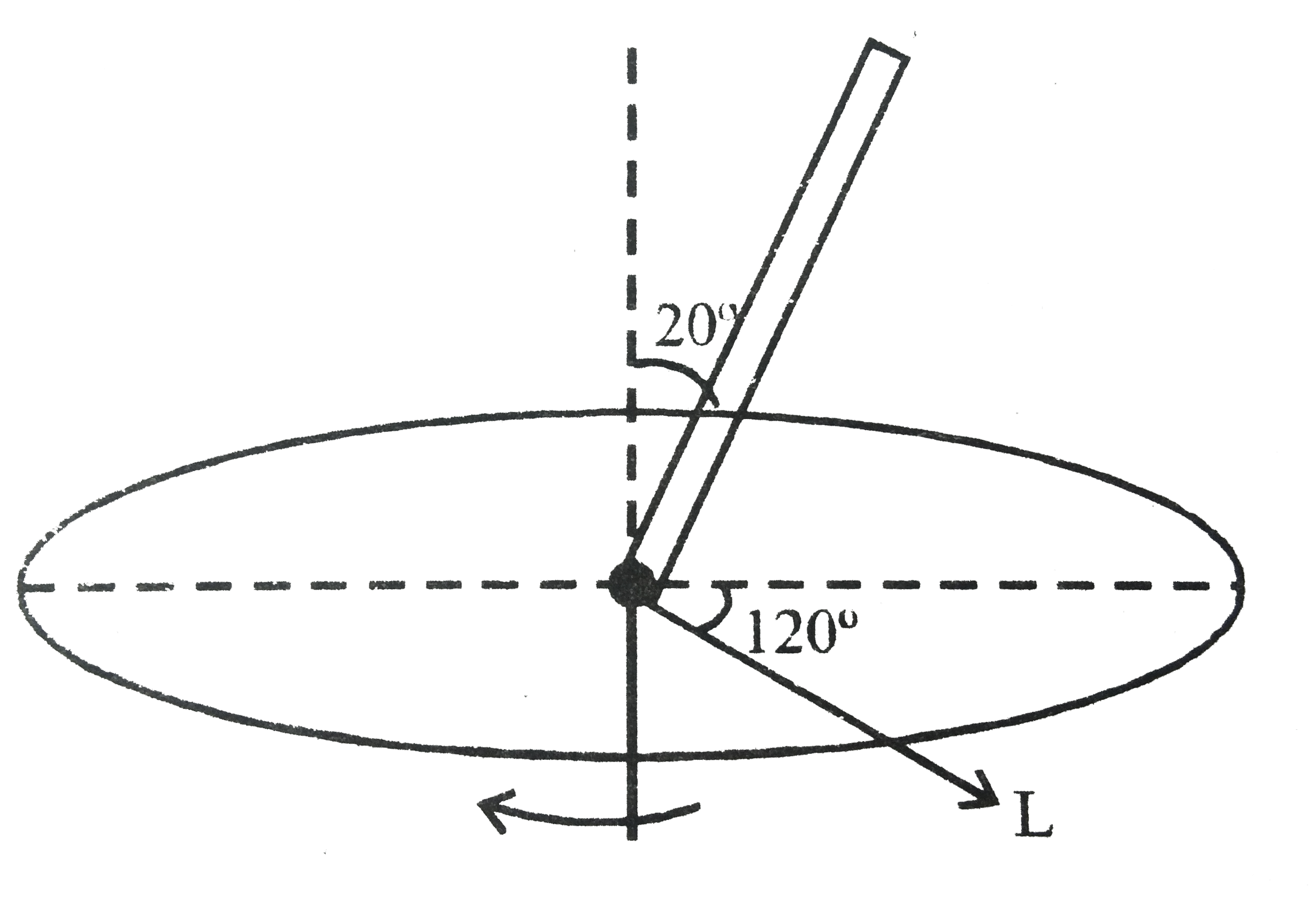
From the relation →L=→r×→p,→L will be ⊥ to r and p, therefore it's direction will be 20∘, down to horizontal.
 .
.
Similar Questions
A thin uniform copper rod of length l and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. Determine the tension in the rod as a function of the distance r from the rotation axis. Find the elongation of the rod.
View SolutionA uniform rod of mass m and length l0 is rotating with a constant angular speed ω about a vertical axis passing through its point of suspension. Find the moment of inertia of the rod about the axis of rotation if it make an angle θ to the vertical (axis of rotation).
View Solution
Knowledge Check
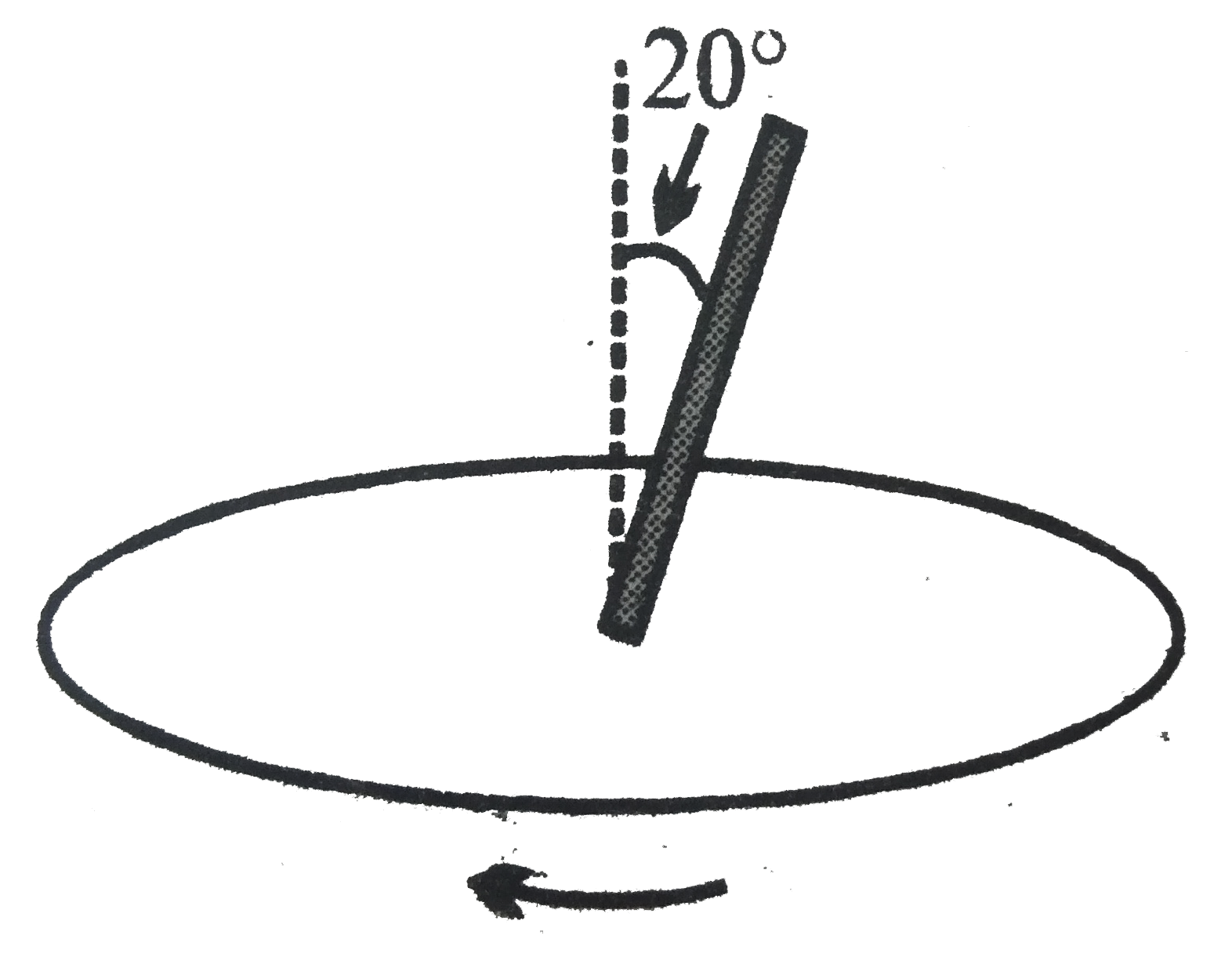
A uniform rod is fixed to a rotating turntable so that its lower end is on the axis of the turntable and it makes an angle of 20% to the vertical. (The rod is thus rotating with uniform angular velocity about a vertical axis passing through one end.) If the turntable is rotating clockwise as seen from above.
 .
.
Is there a torque acts on it, and it so in what direction ?Ayes, verticallyByes horizontallyCyes at 20∘ to the horizonalDnoA rod is rotating with angular velocity ω about axis AB. Find cosθ.
 Ag2lω2Bglω2C2g(lω)2D3g2lω2
Ag2lω2Bglω2C2g(lω)2D3g2lω2A uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A12mω2xB12mω2(1−x2l)C12mω2l(1−x2l2)D12mω2l[1−xl]
A uniform metal rod is rotated in horizontal plane about a vertical axis passing through its end at uniform rate. The tension in the rod is
View SolutionThe radius of gyration of a uniform rod of length l about an axis passing through one of its ends and perpendicular to its length is
View SolutionA thin uniform rod of mass m and length L rotates with the constant angular velocity ω about .the vertical axis passing through the rod's suspensjon point O. It describes a carried surface, then:
View SolutionA thin uniform copper rod of length l and cross-section area A and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. The elongation of the rod will be
View Solutionif rod is rotated about an axis passing through its mid-point , the potential difference between the ends of rod is
View Solution