A weightless rod is acted on by upward parallel forces of 2N and 4N ends A and B respectively. The total leng th of the rod AB=3m. To keep the rod in equilibrium a fo rce of 6N should act in the following manner :
Downwards at any point between A and B.
Downward at mid point of AB.
Downward at a point C such that AC=1m.
Downward at a point D such that BD=1m.
The correct Answer is:D
To solve the problem of keeping the weightless rod in equilibrium under the influence of the given forces, we need to analyze the forces and torques acting on the rod.
1. Identify the Forces Acting on the Rod:
- A force of 2N acts upward at point A (left end of the rod).
- A force of 4N acts upward at point B (right end of the rod).
- We need to apply a force of 6N at a distance x from point B.
2. Determine the Length of the Rod:
- The total length of the rod AB is given as 3m.
3. Set Up the Torque Equation:
- To keep the rod in rotational equilibrium, the sum of the torques about any point must be zero. We will take torques about point B for convenience.
- The torque due to the 2N force at point A (which is 3m from point B) is:
\(
\text{Torque from } A = 2 N \times 3 m = 6 N \cdot m \text{ (counterclockwise)}
\)
- The torque due to the 6N force applied at a distance x from point B (which is 3−x meters from point A) is:
\(
\text{Torque from } 6 N = 6 N \times (3 - x) \text{ (clockwise)}
\)
4. Set the Torques Equal for Equilibrium:
- For the rod to be in equilibrium, the torques must balance:
\(
6 N \cdot m = 6 N \times (3 - x)
\)
5. Solve for x:
- Simplifying the equation:
\(
6 = 6 \times (3 - x)
\)
\(
1 = 3 - x
\)
\(
x = 3 - 1 = 2 \text{ m}
\)
6. Conclusion:
- The force of 6N should be applied 2m from point B to keep the rod in equilibrium.
- A force of 2N acts upward at point A (left end of the rod).
- A force of 4N acts upward at point B (right end of the rod).
- We need to apply a force of 6N at a distance x from point B.
- The total length of the rod AB is given as 3m.
- To keep the rod in rotational equilibrium, the sum of the torques about any point must be zero. We will take torques about point B for convenience.
- The torque due to the 2N force at point A (which is 3m from point B) is:
\(
\text{Torque from } A = 2 N \times 3 m = 6 N \cdot m \text{ (counterclockwise)}
\)
- The torque due to the 6N force applied at a distance x from point B (which is 3−x meters from point A) is:
\(
\text{Torque from } 6 N = 6 N \times (3 - x) \text{ (clockwise)}
\)
- For the rod to be in equilibrium, the torques must balance:
\(
6 N \cdot m = 6 N \times (3 - x)
\)
- Simplifying the equation:
\(
6 = 6 \times (3 - x)
\)
\(
1 = 3 - x
\)
\(
x = 3 - 1 = 2 \text{ m}
\)
- The force of 6N should be applied 2m from point B to keep the rod in equilibrium.
Similar Questions
Determine the point of application of third force for which body is in equillibrium when forces of 20 N & 30 N are acting on the rod as shown in figure
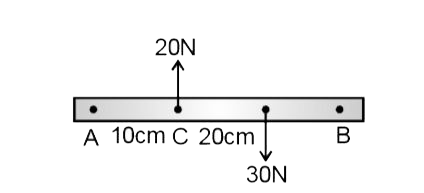
View SolutionTwo parallel unlike forces of magnitudes 15 N and 10 N are acting at point A and B respectively. If C is the point of action of resultant, then AB/BC is
View Solution
Knowledge Check
A weightless rod is acted on by upward parallel forces of 2N and 4N ends A and B respectively. The total leng th of the rod AB=3m. To keep the rod in equilibrium a fo rce of 6N should act in the following manner :
Adownward at any point between A and BBdownward at the midpoint of ABCdownward at a point C such that AC=1 mDdownward at a point D such that BD=1mFour rods AB, BC, CD and DA have mass m,2m,3m and 4m respectively. The center of mass of all the four rods
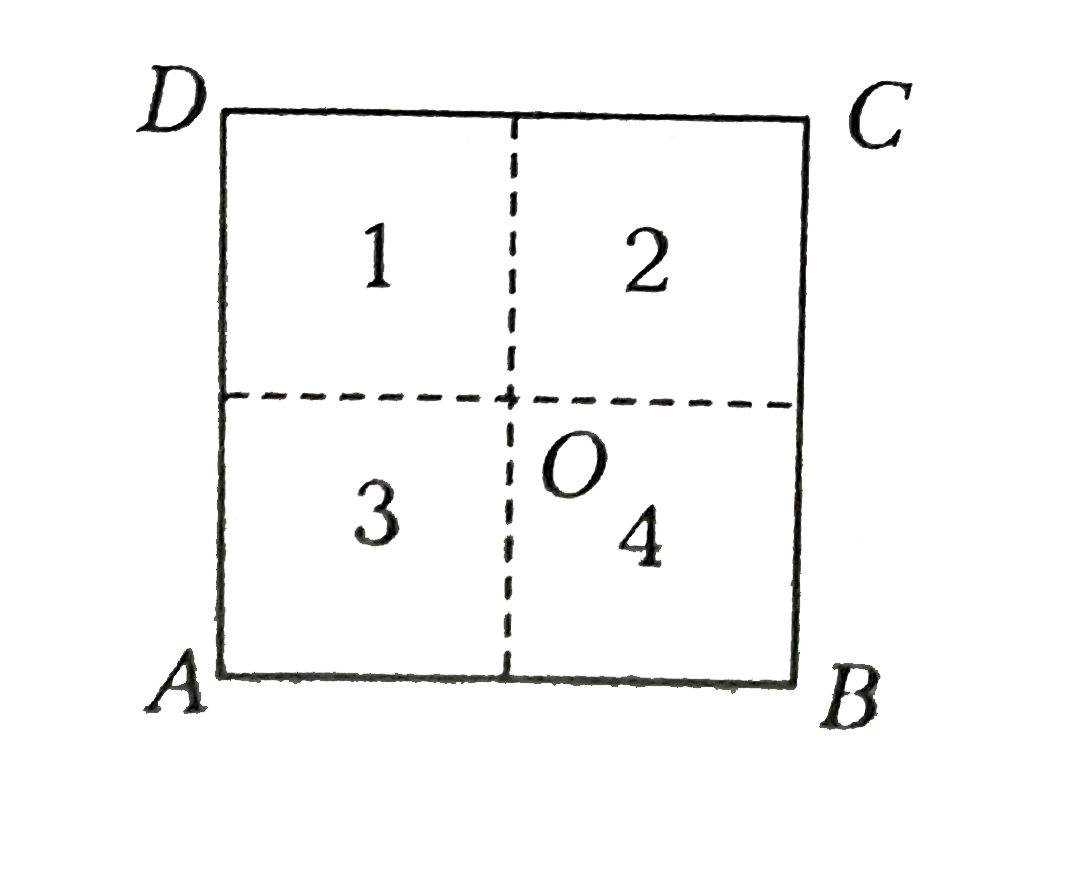 Alie in region 1Blie in region 2Clie in region 3Dlie at 0
Alie in region 1Blie in region 2Clie in region 3Dlie at 0Two like parallel force 20 N and 30 N act at the ands A and B of a rod 1.5 m long. The resultant of the forces will act at the point
A90 cm from AB75 cm from BC20 cm from BD85 cm from A
Two parallel unlike forces of magnitudes 15 N and 10 N are acting at point A and B respectively. If C is the point of action of resultant, then AB/BC is
View SolutionFive forces 2N,√3N,5N,√3Nand2N respectively act at a particle P as shown in the fig
View SolutionA particle is acted on by forces 1, 2,3 and 4 N parallel to the side of a rectangle taken in order. Find resultant.
View SolutionTwo like parallel forces 5 Nand 15 N, act on a light rod at two points A and B respectively, 6 m apart. The resultant force and the distance of its point of action from the point A'are
View SolutionA rod of length L and mass M is acted on by two unequal forces F1 and F2(<F)as shown in the figure.
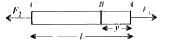
The tension in the rod at a distance y from the end A is given by
View Solution
