Two like parallel force 20 N and 30 N act at the ands A and B of a rod 1.5 m long. The resultant of the forces will act at the point
90 cm from A
75 cm from B
20 cm from B
85 cm from A
The correct Answer is:A
To solve the problem of finding the point where the resultant of two like parallel forces (20 N and 30 N) acts on a rod of length 1.5 m, we can follow these steps:
Step 1: Understand the Forces and Their Positions
We have two forces acting on the ends of a rod:
- A force of 20 N at point A (left end).
- A force of 30 N at point B (right end).
The length of the rod is 1.5 m.
Step 2: Define the Distance from Point A
Let the distance from point A to the point where the resultant force acts be denoted as x. Consequently, the distance from point B to the same point will be 1.5−x.
Step 3: Calculate the Torque About Point A
The torque due to the 20 N force about point A is:
τA=20×x
The torque due to the 30 N force about point A is:
τB=30×(1.5−x)
Step 4: Set Up the Torque Equation
For the system to be in equilibrium, the sum of the clockwise torques must equal the sum of the counterclockwise torques. Therefore, we can set up the equation:
20x=30(1.5−x)
Step 5: Solve for x
Expanding the right side:
20x=45−30x
Now, add 30x to both sides:
20x+30x=45
50x=45
Now, divide both sides by 50:
x=4550=0.9 m
Step 6: Convert to Centimeters
To convert meters to centimeters, multiply by 100:
x=0.9×100=90 cm
Conclusion
The resultant force will act at a point 90 cm from point A.
We have two forces acting on the ends of a rod:
- A force of 20 N at point A (left end).
- A force of 30 N at point B (right end).
The length of the rod is 1.5 m.
Let the distance from point A to the point where the resultant force acts be denoted as x. Consequently, the distance from point B to the same point will be 1.5−x.
The torque due to the 20 N force about point A is:
τA=20×x
The torque due to the 30 N force about point A is:
τB=30×(1.5−x)
For the system to be in equilibrium, the sum of the clockwise torques must equal the sum of the counterclockwise torques. Therefore, we can set up the equation:
20x=30(1.5−x)
Expanding the right side:
20x=45−30x
Now, add 30x to both sides:
20x+30x=45
50x=45
Now, divide both sides by 50:
x=4550=0.9 m
To convert meters to centimeters, multiply by 100:
x=0.9×100=90 cm
The resultant force will act at a point 90 cm from point A.
Similar Questions
Two constant forces 4 N and 5 N act on a body in opposite directions .Find the resultant force on the body
View SolutionA uniform metallic rod AB of length 1.4 m is lifted by two forces P and Q acting along the directions as shown in the figure. If the magnitudes of P and Q are 20 N and 50 N, respectively, find the magnitude and the position of the resultant normal force that acts on the rod.

View Solution
Knowledge Check
Two unlike parallel forces 2 N and 16 N act at the ends of a uniform rod of 21 cm length . The point where the resultant of these two act is at a distance of _________ cm from the greater force.
A1B2C3D4Two like parallel forces 5 Nand 15 N, act on a light rod at two points A and B respectively, 6 m apart. The resultant force and the distance of its point of action from the point A'are
A10N,4.5mB20N,4.5mC20N,1.5mD10N,1.5mLet two like parallel forces are acting, at points A and B such that the force at A is double than the force at B. If C is the point of action of the resultant, then AC/BC IS
A2B1/2C1/3D1/4
Two like parallel forces acting on a rod, 15 N and 5 N are separated by a distance of 4 m. What is the magnitude, direction and point of application of the resultant?
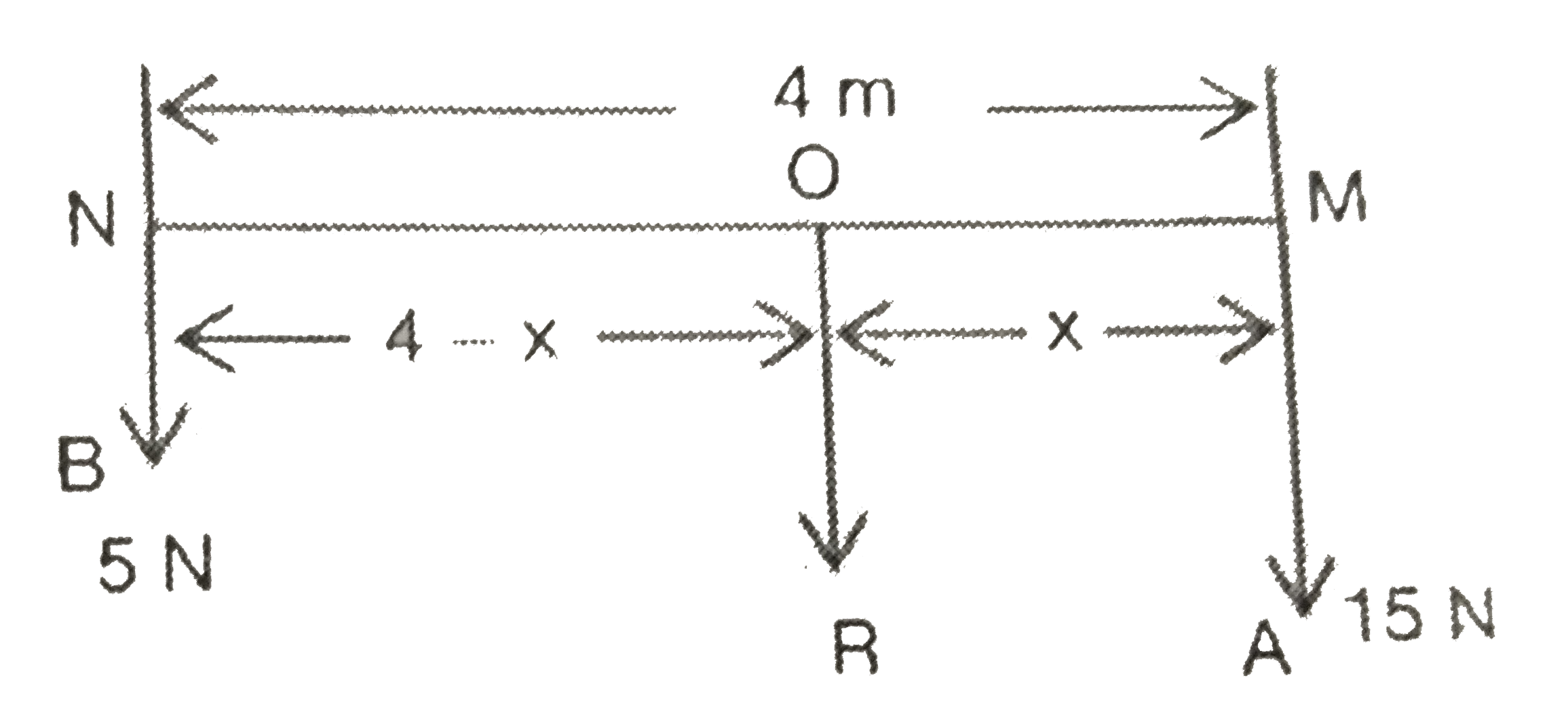
View SolutionLet two like parallel forces are acting, at points A and B such that the force at A is double than the force at B. If C is the point of action of the resultant, then AC/BC IS
View SolutionTwo forces 10 N and 15 N are acting on a body then which cannot be the resultant of these two forces
View SolutionIf two like parallel forces of PQN and QPN have a resultant 2N, then :
View SolutionIf two like parallel forces of PQN and QPN have a resultant 2N, then :
View Solution