Two unlike parallel forces 2 N and 16 N act at the ends of a uniform rod of 21 cm length . The point where the resultant of these two act is at a distance of _________ cm from the greater force.
1
2
3
4
The correct Answer is:C
To solve the problem of finding the distance from the greater force where the resultant of two unlike parallel forces acts, we can follow these steps:
1. Identify the Forces and Their Positions:
- We have two forces: F1=2N (acting at one end of the rod) and F2=16N (acting at the other end).
- The length of the rod is L=21cm.
2. Determine the Resultant Force:
- Since the forces are unlike, the resultant force R can be calculated as:
R=F2−F1=16N−2N=14N
3. Set Up the Equation for Moments:
- Let x be the distance from the greater force (16 N) to the point where the resultant acts.
- The distance from the smaller force (2 N) to the point where the resultant acts will then be 21−x.
- According to the principle of moments (taking moments about the point where the 16 N force acts), we have:
Moment due to 2N=Moment due to 14N
2N×(21−x)=14N×x
4. Simplify the Equation:
- Expanding the equation gives:
42−2x=14x
- Rearranging the equation results in:
42=14x+2x
42=16x
5. Solve for x:
- Dividing both sides by 16 gives:
x=4216=2.625cm
6. Final Calculation:
- Since we need the distance from the greater force (16 N), we find that:
x≈2.625cm
Conclusion:
The point where the resultant of these two forces acts is approximately 2.625 cm from the greater force (16 N).
- We have two forces: F1=2N (acting at one end of the rod) and F2=16N (acting at the other end).
- The length of the rod is L=21cm.
- Since the forces are unlike, the resultant force R can be calculated as:
R=F2−F1=16N−2N=14N
- Let x be the distance from the greater force (16 N) to the point where the resultant acts.
- The distance from the smaller force (2 N) to the point where the resultant acts will then be 21−x.
- According to the principle of moments (taking moments about the point where the 16 N force acts), we have:
Moment due to 2N=Moment due to 14N
2N×(21−x)=14N×x
- Expanding the equation gives:
42−2x=14x
- Rearranging the equation results in:
42=14x+2x
42=16x
- Dividing both sides by 16 gives:
x=4216=2.625cm
- Since we need the distance from the greater force (16 N), we find that:
x≈2.625cm
The point where the resultant of these two forces acts is approximately 2.625 cm from the greater force (16 N).
Topper's Solved these Questions
- SIMPLE MACHINESBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - SIMPLE MACHINESEXERCISE - Level- 2
25 Videos
- SIMPLE MACHINESBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - SIMPLE MACHINESEXERCISE - Level- 3
10 Videos
- SIMPLE MACHINESBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - SIMPLE MACHINESEXERCISE - Essay Type Questions
3 Videos
- MODERN PHYSICSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MODERN PHYSICSEXERCISE - Level 3
5 Videos
- WAVES MOTION AND SOUND BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - WAVES MOTION AND SOUND EXERCISE - Level 3
10 Videos
Similar Questions
Two like parallel forces P and Q act at the ends of a strianght ruler of length l. What is the distance by which the resultant of the forces will shift along the ruler If P is doubled ?
View SolutionTwo forces 3N and 4N are acting on a point O. if angle between these two forces is 90∘ find the resultant of these two forces.
View Solution
Knowledge Check
Two like parallel force 20 N and 30 N act at the ands A and B of a rod 1.5 m long. The resultant of the forces will act at the point
A90 cm from AB75 cm from BC20 cm from BD85 cm from ATwo like parallel forces 5 Nand 15 N, act on a light rod at two points A and B respectively, 6 m apart. The resultant force and the distance of its point of action from the point A'are
A10N,4.5mB20N,4.5mC20N,1.5mD10N,1.5mThe resultant of two like parallel forces 5 N and 10 N is _______ N.
A10B5C15D50
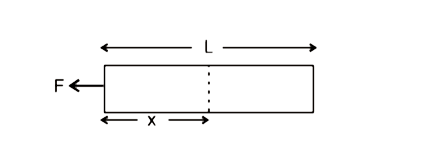
A horizontal force is applied on a uniform rod of length L kept on a frictionless surface. Find the tension in rod at a distance 'x' from the end where force is applied
View SolutionTwo forces of 5N and 7N act on a aprticle with an angle of 60∘ between them. Find the resultant force.
View SolutionTwo forces 25 N and 16 N act on a body of mass 1.0 kg. The minimum acceleration will be
View SolutionTwo forces 25 n and 16 N act on a body of mass 1.0 kg . The minimum acceleration will be
View SolutionTwo forces 25 N and 16 N act on a body of mass 1.0 kg. The minimum acceleration will be
View Solution
