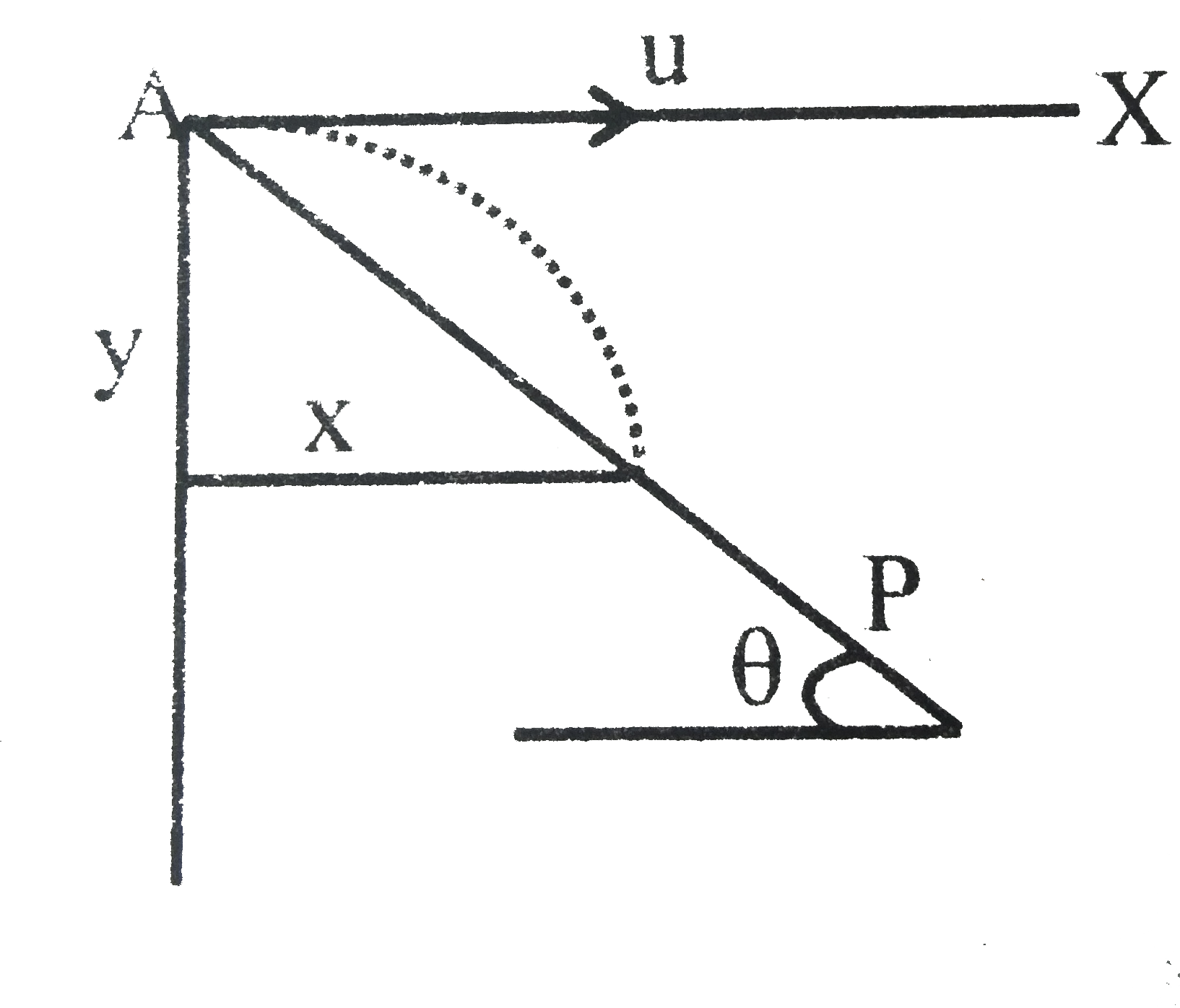
A pariicle is projected horizontally with a speed (u) from top of a plance inclined at anangle $θ$ with the horizontal direction. How far from the point of projection will the particle strike the plane ?

Video Solution

Text Solution

Verified by Experts

Suppose that the particle strikes the plane at a point $P$ with corrdinates $(x, y)$ . Consider the motion between points $A$ and $P$ by resolving them into two directions
Motion in $x$ -direction
Initial velocity $= u$ ,
acceleration $= 0$
$∴ x = u t ... (i)$
Motion in $y$ -direction
Initial velocity $= 0$ ,
acceleration $= g$ ,
y =(½) "gt"^(2) ...(ii)
Eliminating $t$ from (i) & (ii)
$y = \frac{1}{2} \frac{g (x^{2})}{u^{2}}$
Also, $y = x tan θ$
Therefore $\frac{g x^{2}}{2 u^{2}} = x tan θ \Rightarrow \frac{g x^{2}}{2 u^{2}} - x tan θ = 0$
$\Rightarrow x (\frac{g x}{2 u^{2}} - tan θ) = 0 \Rightarrow x \frac{2 u^{2} tan θ}{g} ... (i i i)$
Thus, $y = x tan θ = \frac{2 u^{2} {tan}^{2} θ}{g} ... (i v)$
$∴$ Distance $A P = \sqrt{x^{2} + y^{2}} = \frac{2 u^{2}}{g} tan θ$
$= \sqrt{(1 + {tan}^{2} θ)} = \frac{2 u^{2}}{g} tan θ sec θ$ ,

Updated on:21/07/2023

A ball is projected horizontally with a speed v from the top of the plane inclined at an angle $45^{\circ}$ with the horizontal. How far from the point of projection will the ball strikes the plane?
A $\frac{2 v^{2}}{g}$
B $\sqrt{2} [\frac{2 v^{2}}{g}]$
C $\frac{v^{2}}{g}$
D $\sqrt{2} \frac{v^{2}}{g}$
A particle is projected horizontally with a speed V=5m/s from the top of a plane inclined at an angle $θ = 37^{\circ}$ to the horizontal $(g = 10 m / s^{2})$

How far from the point of projection will the particle strike the plane?
A75m
B $\frac{65}{16} m$
C $\frac{75}{16} m$
D $\frac{85}{9} m$
A particle is projected horizontally with a speed V=5m/s from the top of a plane inclined at an angle $θ = 37^{\circ}$ to the horizontal $(g = 10 m / s^{2})$

Find the time taken by the particle to hit the plane.
A $\frac{3}{4} s$
B $3 s$
C $4 s$
D $\frac{4}{3} s$