A square loop of side 'a' with a capacitor of capacitance C is located between two current carrying long parallel wires as shown. The value of I in the wires in given as .
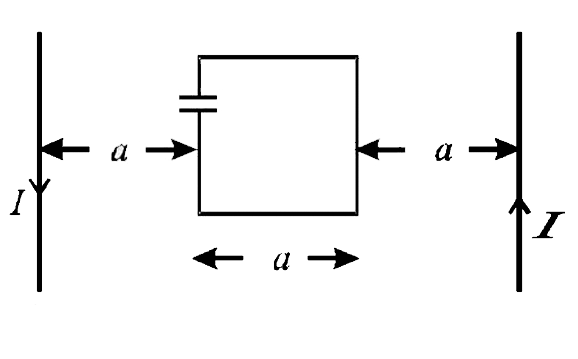
(a) Calculate maximum current in the square loop.
(b) Draw a graph between charges on the upper plates of the capacitor vs time.
The correct Answer is:(a)
(b)
(a) Magnetic flux through loop
Similar Questions
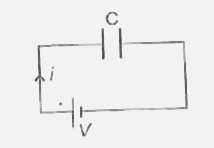
At a particle state the current in the circuit given below is i. The displacement current between the plates of the capacitor shown below is
View SolutionA square loop of conducting wire is placed symmetrically near a long straight current carrying wire as shown. Match the statement in column-I with the corresponding results in column-II

View Solution
Knowledge Check
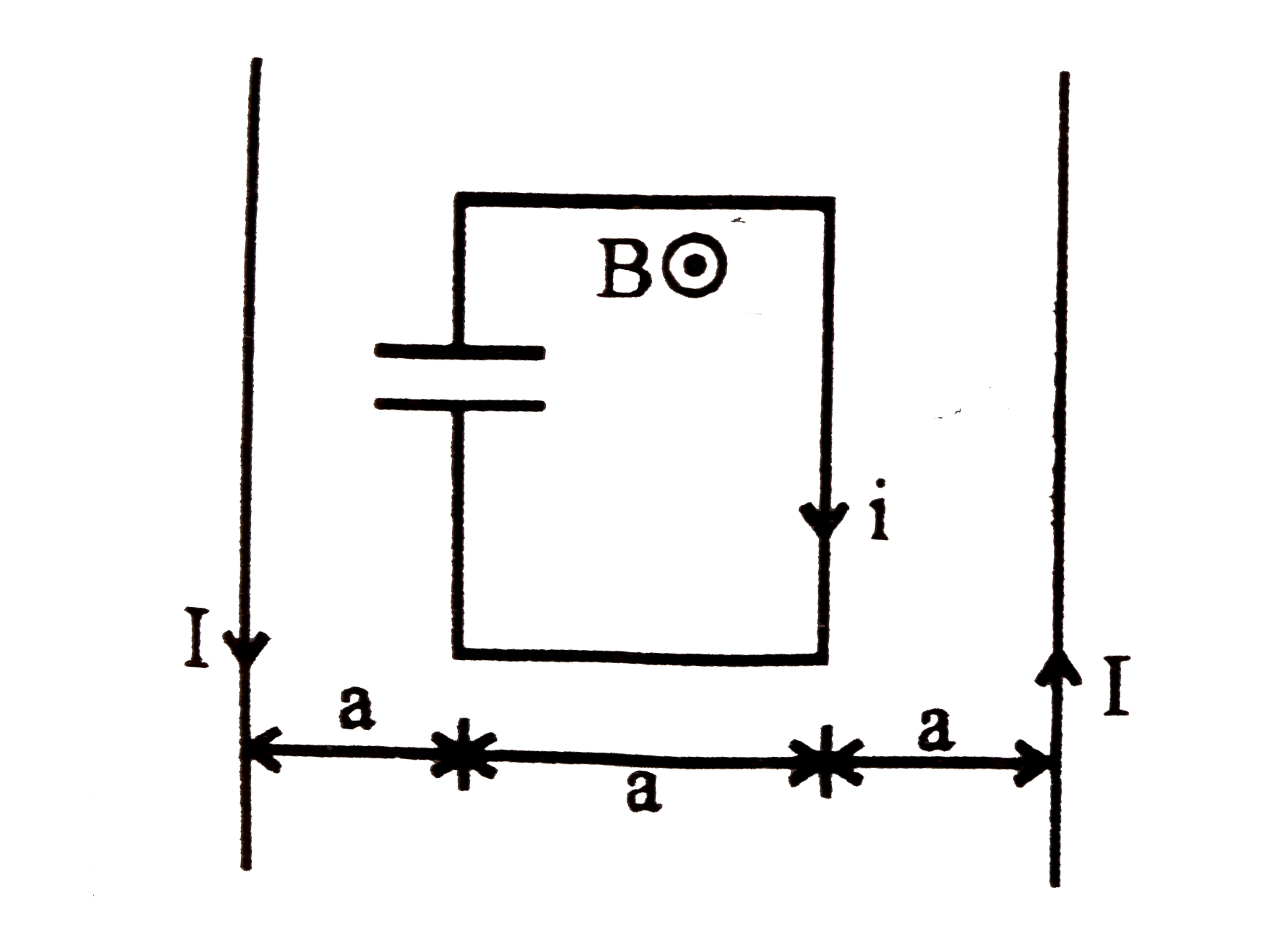
In fig, a square loop consistaing of an inductor of inductance L and resistor of resistance R is placed between two long parallel wires. The two long straight wires have time - varing current of magnitude I=(I0)cosωt but the direction of current in them are opposite
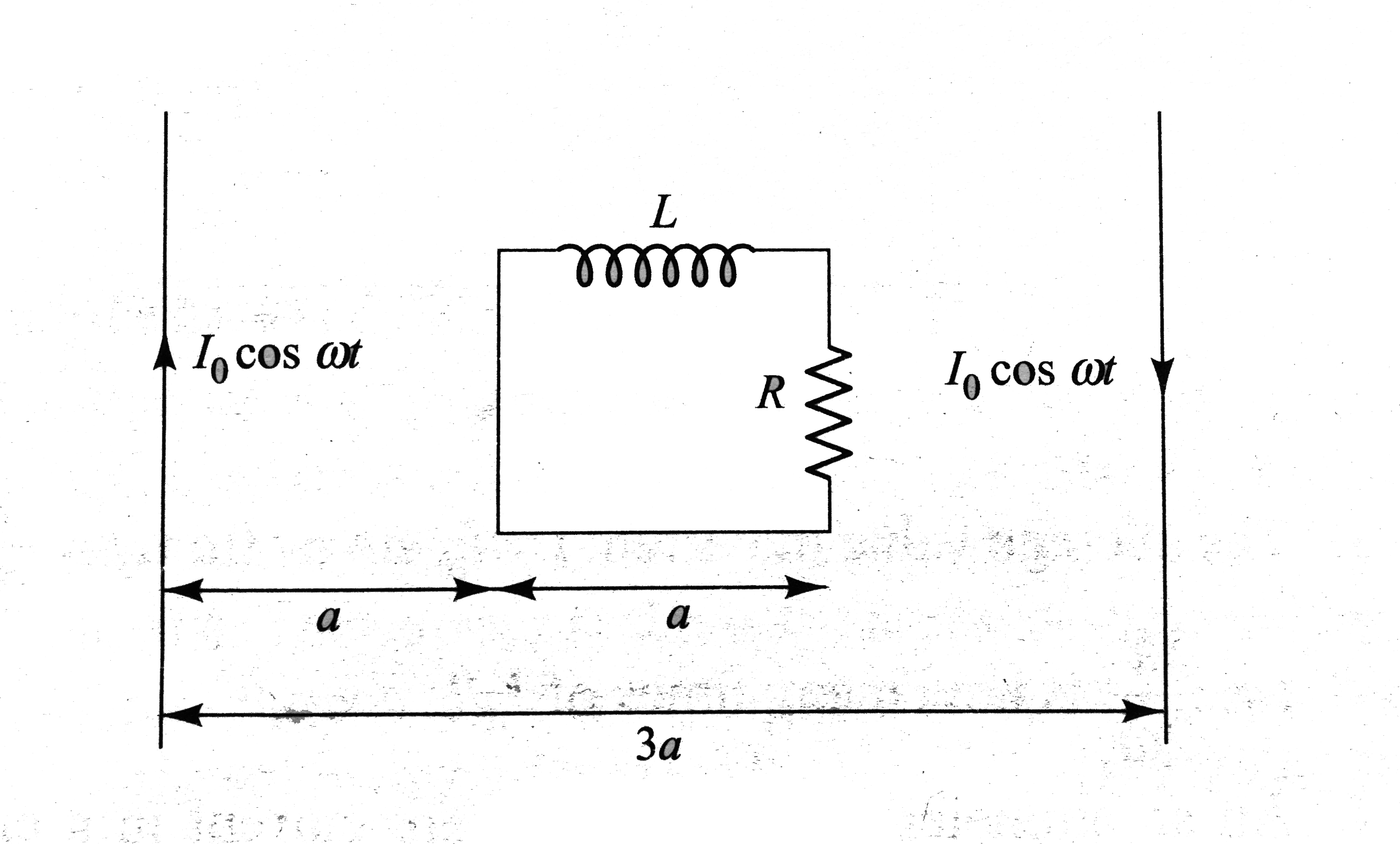
A2μ0a1n2I0ωπ√R2(+ω2L2)sin(ωt−ϕ)B2μ0a1n2I0ωπ√R2(+ω2L2)sin(ωt+ϕ)C2μ0a1n2I0ωπ√R2(+ω2L2)sin(ωt)Dμ0a1n2I0ωπ√R2+ω2L2sin(ωt−ϕ)A rectangular loop is placed to the left of large current carrying straight wire as shown in Figure. Current varies with time as I=2t. Find direction of induced current Iin in the square loop.
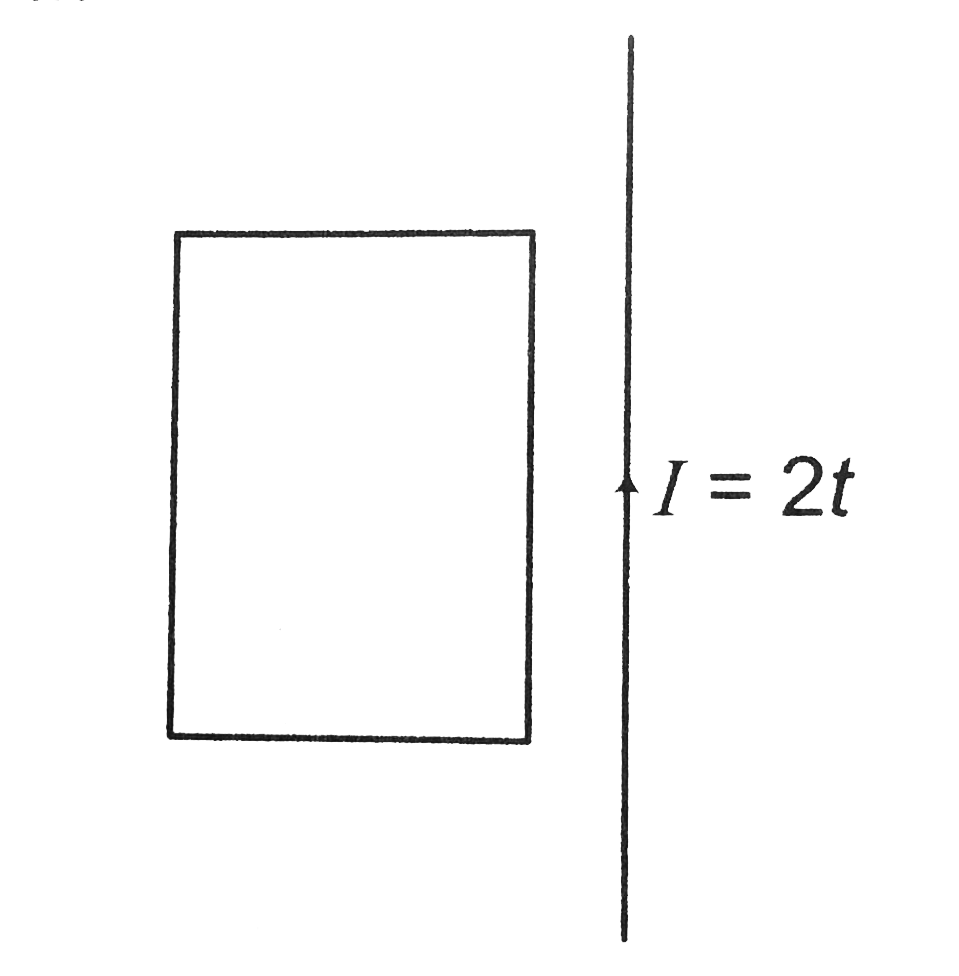 Ain complete informationBNot inducedCAnticlockwiseDClockwise
Ain complete informationBNot inducedCAnticlockwiseDClockwiseIn fig, a square loop consisting of an inductor of inductance L and resistor of resistance R is placed between two long parallel wires. The two long straight wires have time - varying current of magnitude I=(I0)cosωt but the direction of current in them are opposite
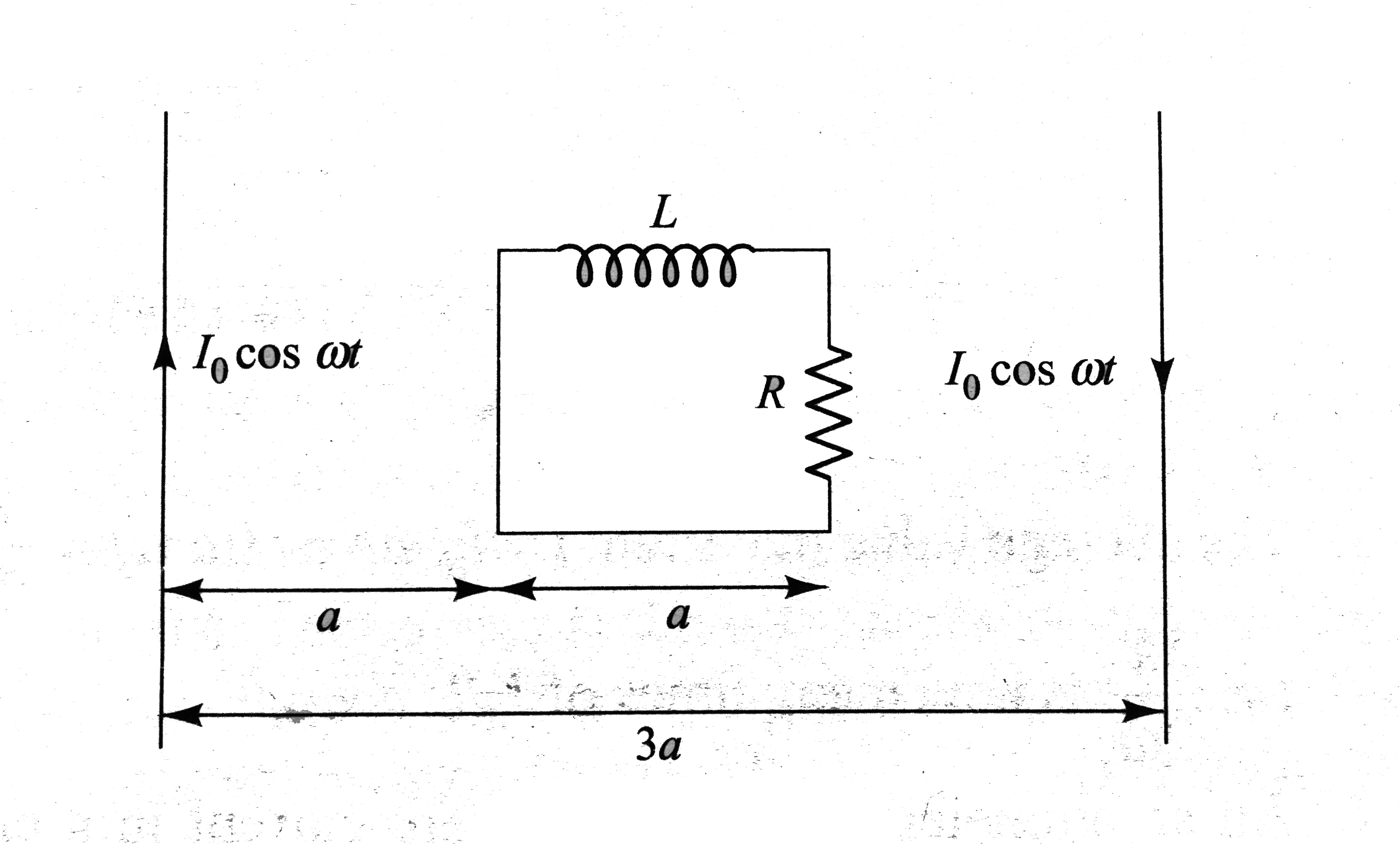
Total magnetic flux in this loop isAμ0Iaπ1n2B2μ0Iaπ1n2C4μ0Iaπ1n2Dμ0Ia2π1n2
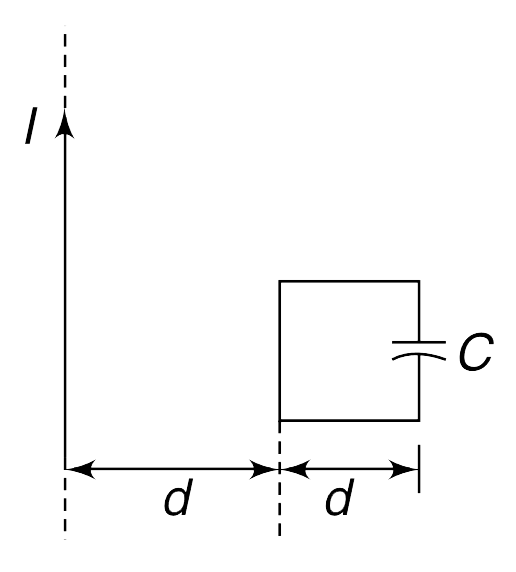
A square loop of side length d has a capacitor of capacitance C and the resistance of the loop is R. In the plane of the loop there is a long straight current carrying wire having current I. The distance of the straight wire from the loop is d as shown in figure. The current in the straight wire is made to grow with time as I=αt where α=2As−1. Neglect self inductance of the loop.
(a) Find the charge on the capacitor as a function of time (t).
(b) Find the heat generated in the loop as a function of time.
(c) Who supplies energy for heat dissipation?
View SolutionAn ac source of emf V=V0sinωt is connected to a capacitor of capacitance C. Deduce the expression for the current (I) flowing in it. Plot the graph of (i) Vvs.ωt,and (ii) Ivs.ωt
View SolutionA square loop of side l carries a current i. it is placed as shown in figure. Find the magnetic moment of the loop.
View SolutionIn fig, a square loop consistaing of an inductor of inductance L and resistor of resistance R is placed between two long parallel wires. The two long straight wires have time - varing current of magnitude I=(I0)cosωt but the direction of current in them are opposite
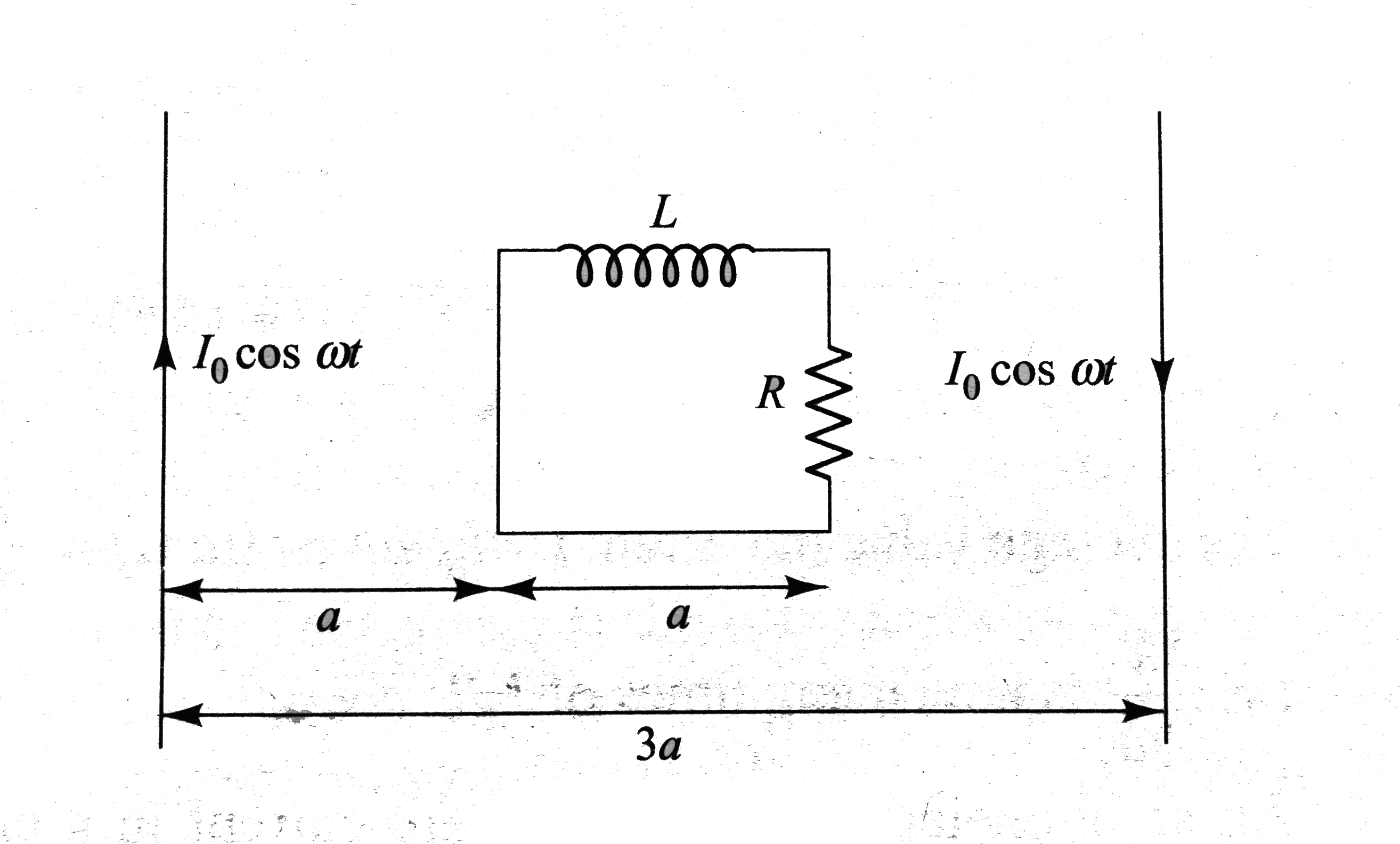
Magnitude of emf in this circuit only due to flux change associated with two long straight current carrying wires will be
View SolutionA square loop of side a is placed at a distance a length away from a long wire carrying a current I1 . If the loop carries a current I2 as shown in the figure . Then the nature of the nature of the force and its amount is

View Solution
