In fig, a square loop consistaing of an inductor of inductance L and resistor of resistance R is placed between two long parallel wires. The two long straight wires have time - varing current of magnitude I=(I0)cosωt but the direction of current in them are opposite
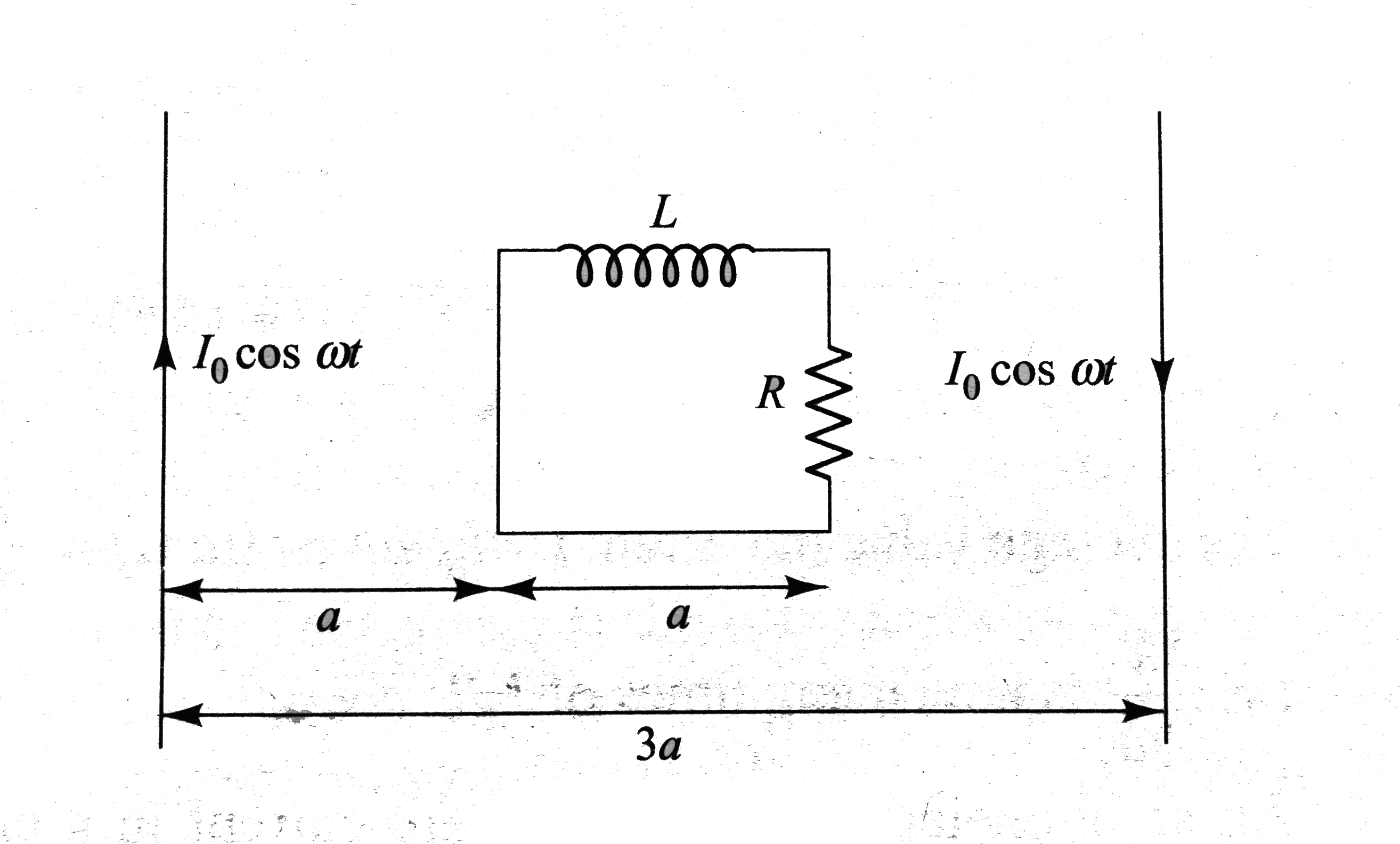
Magnitude of emf in this circuit only due to flux change associated with two long straight current carrying wires will be
μ0a1n2I0ωπsinωt
2μ0a1n2I0ωπsinωt
μ0a1n2I0ω2πcosωt
μ0a1n2I0ωπcosωt
The correct Answer is:A
dϕ=BdA
dϕ=[μ0I2πx+μ0I2π(3a−x)]adx

ϕ=μ0I2π[∫2aadxx+∫2aadx(3a−x)]a,ϕ=μ0Iaπ1n2.
Meagnitude of emf in this circuit:
ε=∣∣∣dϕdt∣∣∣=μ0a(1n2)π∣∣∣dIdt∣∣∣
μ0a1n2I0ωπsinωt .
ac current , I=μ0a1n2I0ωπ√R2+ω2L2sin(ωt−ϕ).
Topper's Solved these Questions
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICSCHAPTER - ALTERNATING CURRENTEXERCISE - Exercises Integer
4 Videos
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICSCHAPTER - ALTERNATING CURRENTEXERCISE - Archives Subjective
1 Videos
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICSCHAPTER - ALTERNATING CURRENTEXERCISE - Exercises Assertion-reasoning
7 Videos
- OSCILLATIONSBOOK - CENGAGE PHYSICSCHAPTER - OSCILLATIONSEXERCISE - QUESTION BANK
39 Videos
- ATOMIC PHYSICSBOOK - CENGAGE PHYSICSCHAPTER - ATOMIC PHYSICSEXERCISE - ddp.4.3
15 Videos
Similar Questions
A square loop of side 'a' with a capacitor of capacitance C is located between two current carrying long parallel wires as shown. The value of I in the wires in given as I=(I0)sinωt.
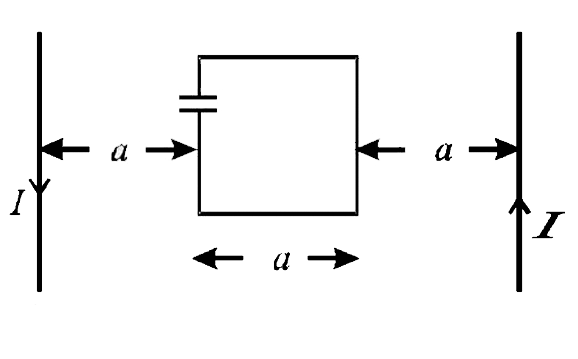
(a) Calculate maximum current in the square loop.
(b) Draw a graph between charges on the upper plates of the capacitor vs time.
View SolutionA square loop is placed near a long straight current carrying wire as shown. Match the following table.
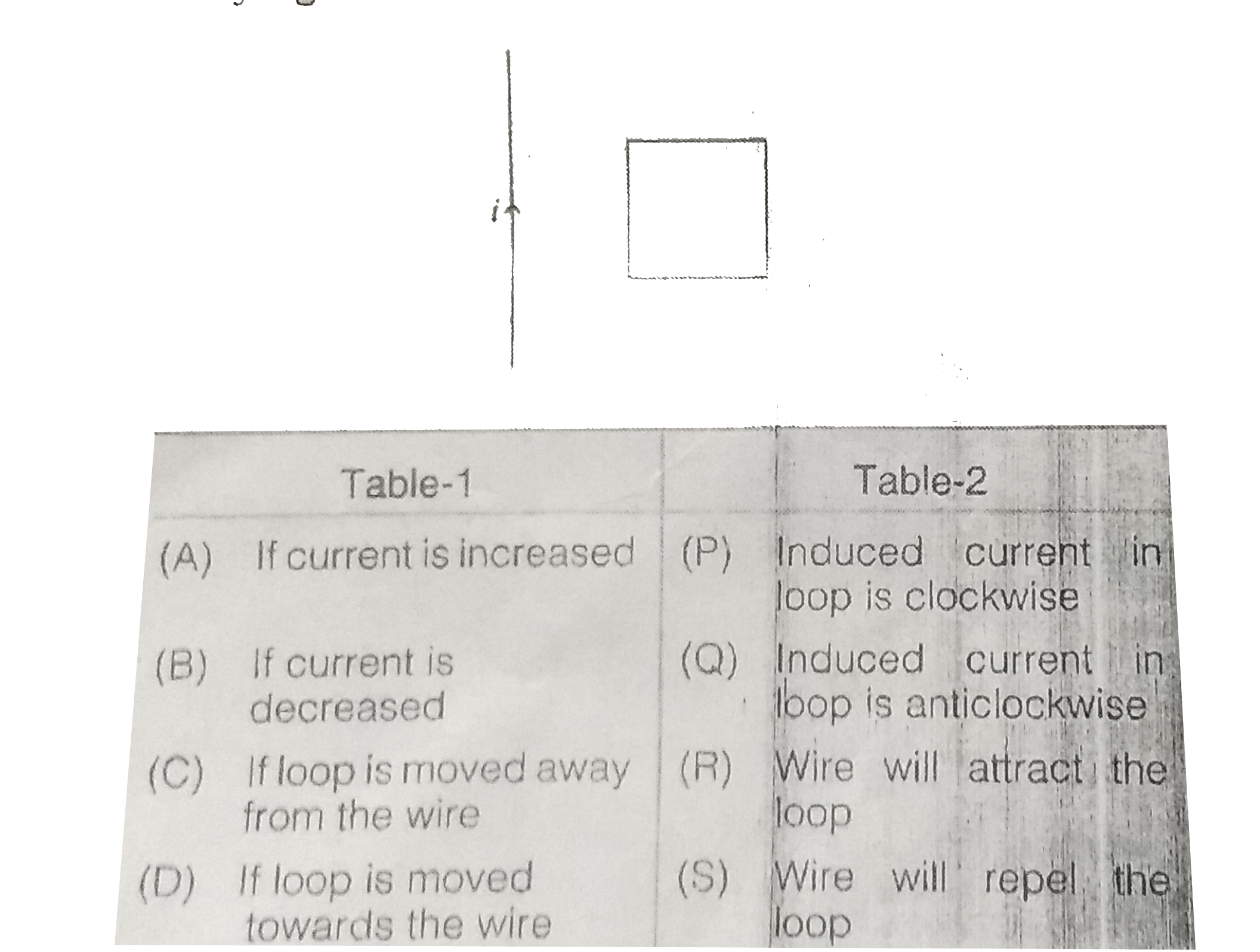
View Solution
Knowledge Check
In fig, a square loop consisting of an inductor of inductance L and resistor of resistance R is placed between two long parallel wires. The two long straight wires have time - varying current of magnitude I=(I0)cosωt but the direction of current in them are opposite
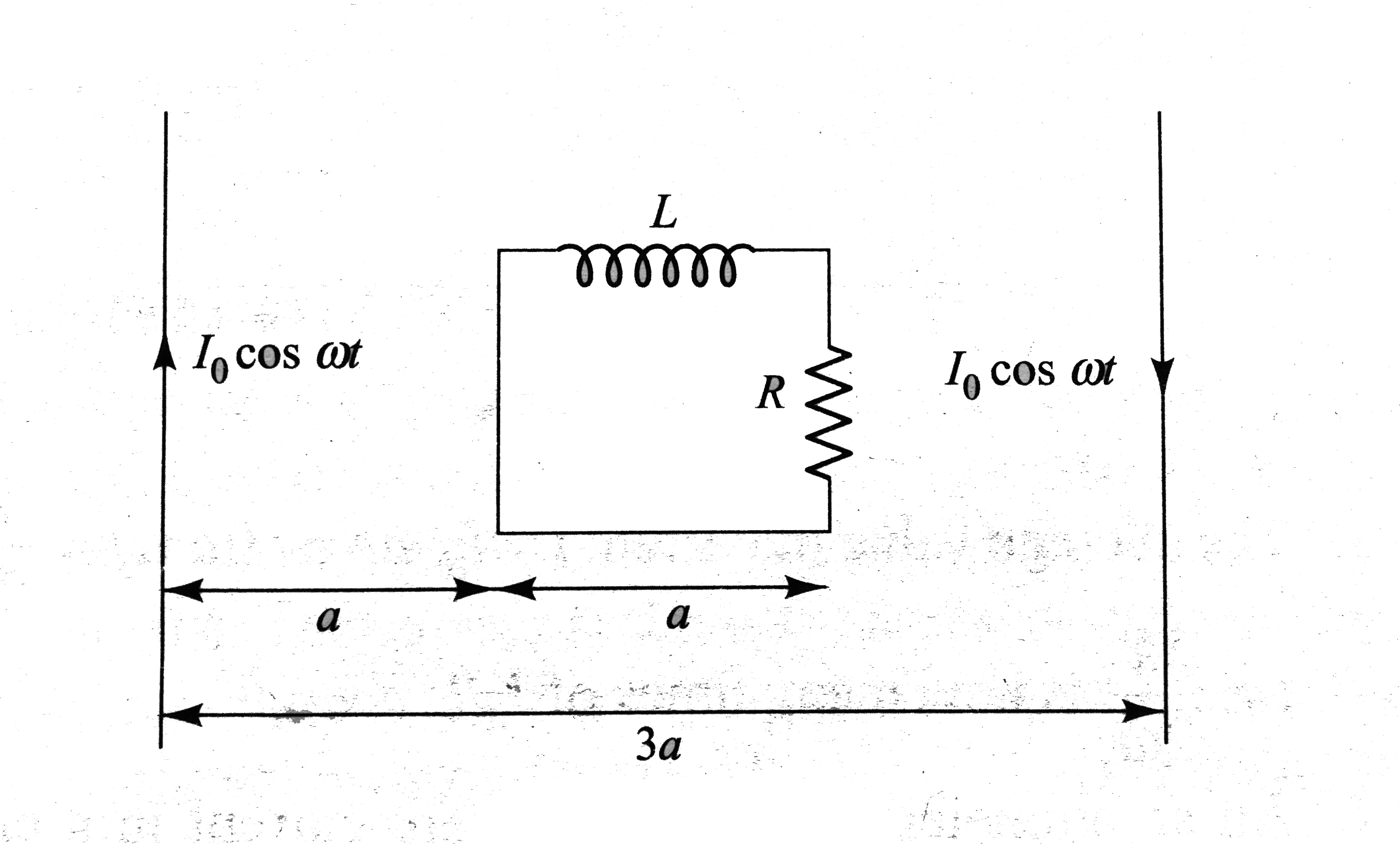
Total magnetic flux in this loop isAμ0Iaπ1n2B2μ0Iaπ1n2C4μ0Iaπ1n2Dμ0Ia2π1n2The field due to a long straight wire carrying a current I is proportional to
AIB√ICI2D1/IA field due to a long straight wire carrying a current I is proportional to
AlBl2Cl3D√l
A long straight wire carries a current of 35 A. What is the magnitude of the field →B at a point 20 cm from the wire?
View SolutionA long straight wire carries a current of 35 A. What is the magnitude of the field →B at a point 20 cm from the wire?
View SolutionThe field due to a long straight wire carrying a current I is proportional to
View SolutionThe field due to a long straight wire carrying a current I is proportional to
View SolutionThe magnetic induction at any point due to a long straight wire carrying a current is
View Solution
