In a L-R decay circuit, the initial current at t=0 is I. The total charge that has flown through the resistor till the energy in the inductor has reduced to one-fourth its initial value, is
The correct Answer is:LI/2R
Initial energy E1=12LI2…(1)
Final energy E2=12LI22…(2)
given that E2=14E1…(3)
From (1),(2) and (3)
12LI22=14×12LI2⇒I2=I2…(4)
For decaying I=I0e−t/τ…(5)
From (4) and (5)
t=τlm2...(6)
Δq=∫t0−Ie−t/τdt=Iτ[e−t/τ]τ0=ILR[e−ln2−1]=LI2R
Similar Questions
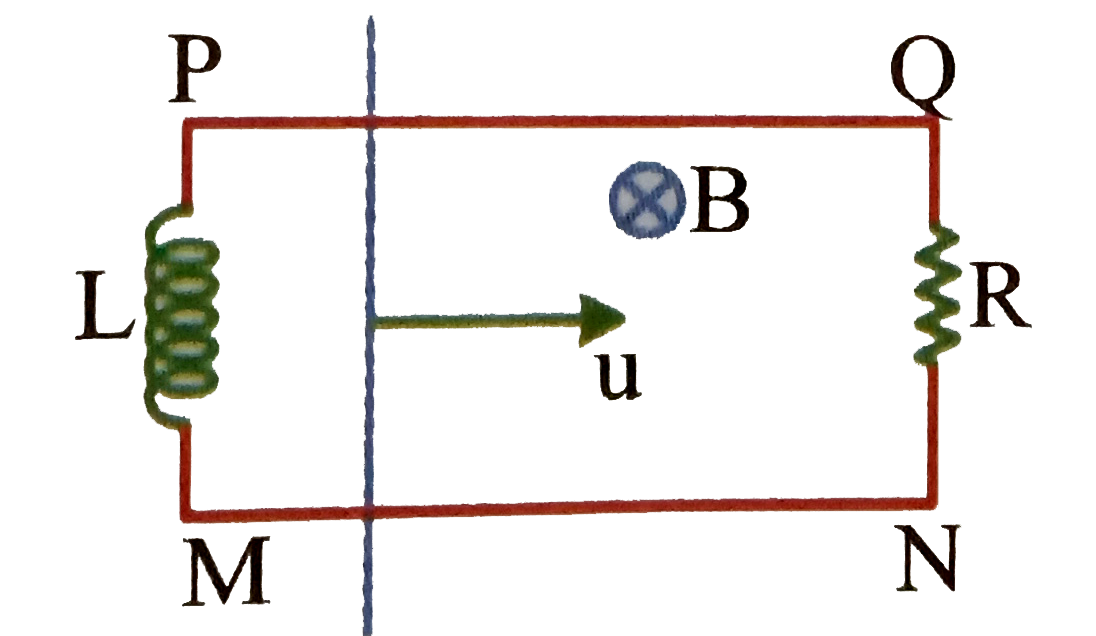
In the figure, a conducting rod of length l=1 meter and mass m=1kg moves with initial velocity u=5m/s. On a fixed horizontal frame containing inductor L=2H and resistance R=1W. PQ and MN are smooth, conducting wires. There is a uniform magnetic field of strength B=1T. Initially there is no current in the inductor. Find the total charge in coulomb, flown through the inductor by the time velocity of rod becomes vf=1m/s and the rod has travelled a distance x=3 meter.
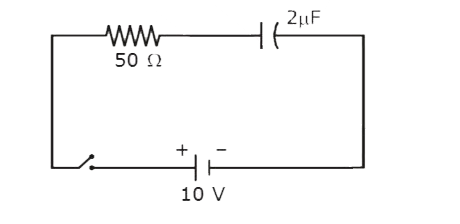
View SolutionFor the circuit shown in figure below, At t = 0, switch is closed, the initial current through resistor and final charge on capacitor are
View Solution
Knowledge Check
In a decaying L−R circuit, the time after which energy stores in the inductor reduces to one fourth of its initial values is
A(ln2)LRB0.5LRC√2LRD(√2√2−1)LRA circuit contains an inductor of value 2H as shown at t=0 no current was flowing through battery. Find the energy stored in inductor at t=4 sec.
 A144JB150JC160JD180J
A144JB150JC160JD180JThe capacitor of capacitance C in the circuit shown in fully charged initially. Resistance is R.–
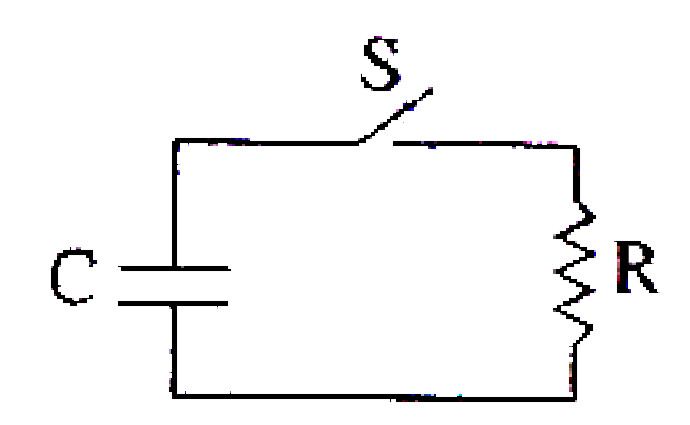
After the switch S is closed, the time taken to reduce the stored energy in the capacitor to half its initial value isARC/2B2RC in 2CRC ln 2DRCln22
For the circuit shown in figure, find
(a) the initial current through each resistor
(b) steady state current through each resistor
(c) final energy stored in the capacitor
(d) time constant of the circuit when switch is opened.

View SolutionThe total heat produced in resistor r in an RL circuit when the current in the inductor decreases from Io to 0 is
View SolutionA charged capacitor of capacitance C is discharging through a resistor of resistance R. At what time the charge on the capacitor is equal to one half of its initial value?
View SolutionLetC be the capacitance of a capacitor discharging through a resistor R. Suppose t1 is the time taken for the energy stored in the capacitor to reduce to half its initial value and t2 is the time taken for the charge to reduce to one-fourth its initial value. Then the ratio t1/t2 will be
View SolutionCurrent flowing through a conducting wire is given by
I=(1+2t)
Where t is in seconds and current I is in amperes. The charge (in coulombs) flown through the resistor in the interval from t=0 to t=1 second is -
View Solution
