Same current I is flowing in three infinitely long wires along x, y and z directions. What is the magnetic field at point (0,0,−a)?
μ0i2πa(ˆj−ˆi)
μ0i2πa(ˆi+ˆj)
μ0i2πa(ˆi−ˆj)
μ0i2πa(ˆi+ˆj+ˆk)
The correct Answer is:A
→B=→B1+→B2
→B=μ04π2Iaˆj+μ04π(−ˆi)
=μ04π2Ia(−ˆi+ˆj)
 .
.
Similar Questions
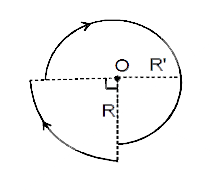
A current of I ampere is flowing through each of the bent wires as shown the magnitude and direction of magnetic field at O is
View SolutionA steady current I flows along an infinitely long straight wire with circular cross-section of radius R. What will be the magnetic field outside and inside the wire at a point r distance far from the axis of wire?
View Solution
Knowledge Check
Same current i is flowing in the three infinitely long wires along positive x-,y- and z-directions. The magnetic filed at a point (0,0,-a) would be
Aμ0i2πa(ˆj−ˆi)Bμ0i2πa(ˆj+ˆi)Cμ0i2πa(ˆi−ˆj)Dμ0i2πa(ˆi+ˆj+ˆk)Same current i is flowing in the three infinitely long wires along positive x-,y- and z-directions. The magnetic filed at a point (0,0,-a) would be
Aμ0i2πa(ˆj−ˆi)Bμ0i2πa(ˆi−ˆj)Cμ0ˆi2πa(ˆi+ˆj)Dμ0i2πa(−ˆi−ˆj)A direct current l flow along the length of an infinitely long striaght thin walled pipe then the magnetic field is
Auniform throughout the pipe but not zeroBzero only along the axis of the pipeCzero at any point inside the pipeDmaximum at the center and minimum at the edge
A current of 10A is established in a long wire along the positive z-axis. Find the magnetic field (vec B) at the point (1m , 0 , 0).
View SolutionAn infinitely long wire carrying current I is bent to from a L shaped wire. Let the bend be the origin and the two arms be along x and y direction (see figure). Calculate the magnitude of magnetic field at point P (in first quadrant) whose co-ordinates are (x, y).

View SolutionA direct current / flows along the length of an infinitely long straight thin walled pipe, then the magnetic field is
View SolutionAssertion : A current I flows along the length of an infinitely long straight and thin walled pipe. Then the magnetic field at any point inside the pipe is zero.
Reason : ∮→B.d→l=μ0I
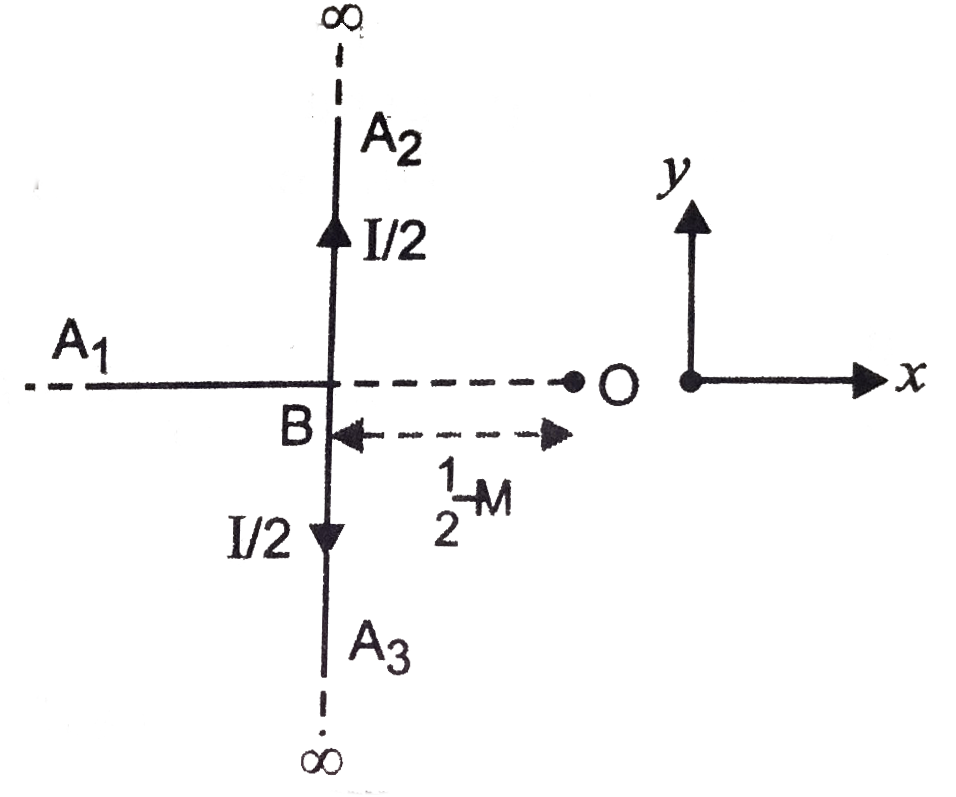
View SolutionA current I=IA flowing through an infinite long wire A1 divides between two infinite long wires A2 and A3 at junction B. The magnitude of the magnetic field at point O due to current through wires is :
View Solution
