The location of three long wires carrying same current I are x=−a, x=0 and x=+ a respectively as shown in figure. The magnetic field at point (0, 0, a) is
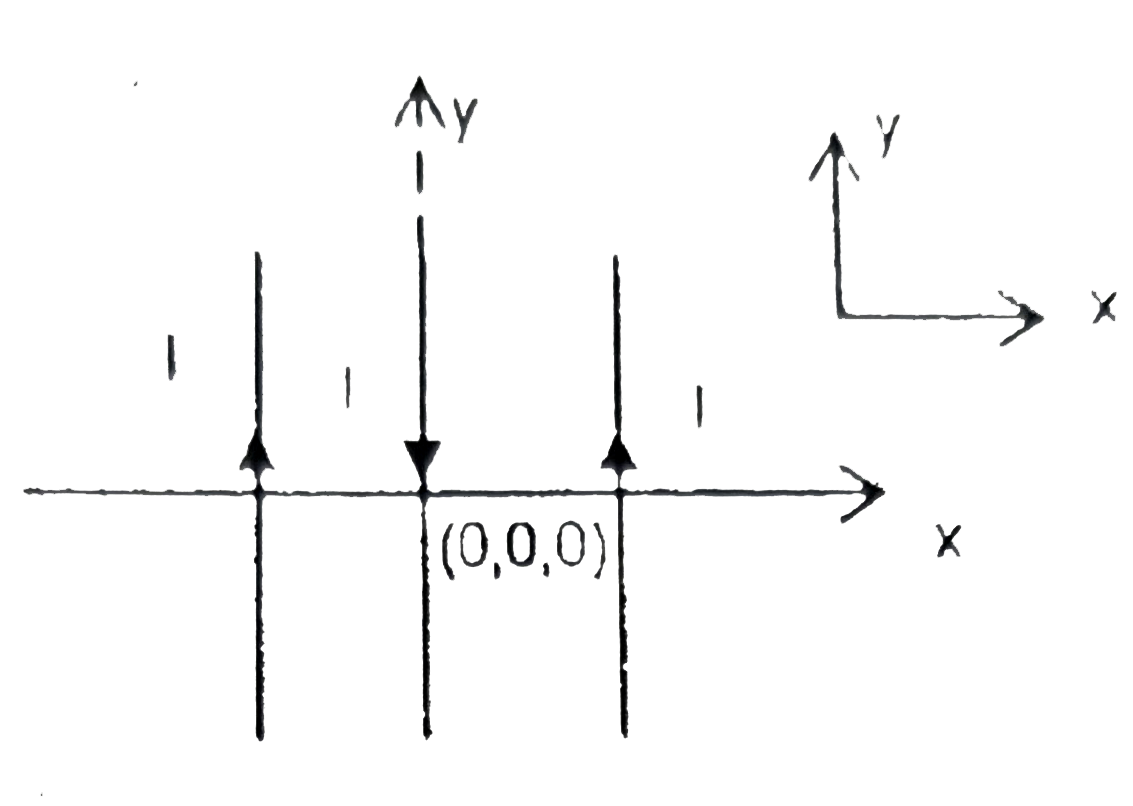
μ0I2πa
μ0I√2πa
μ0I2√2πa
zero
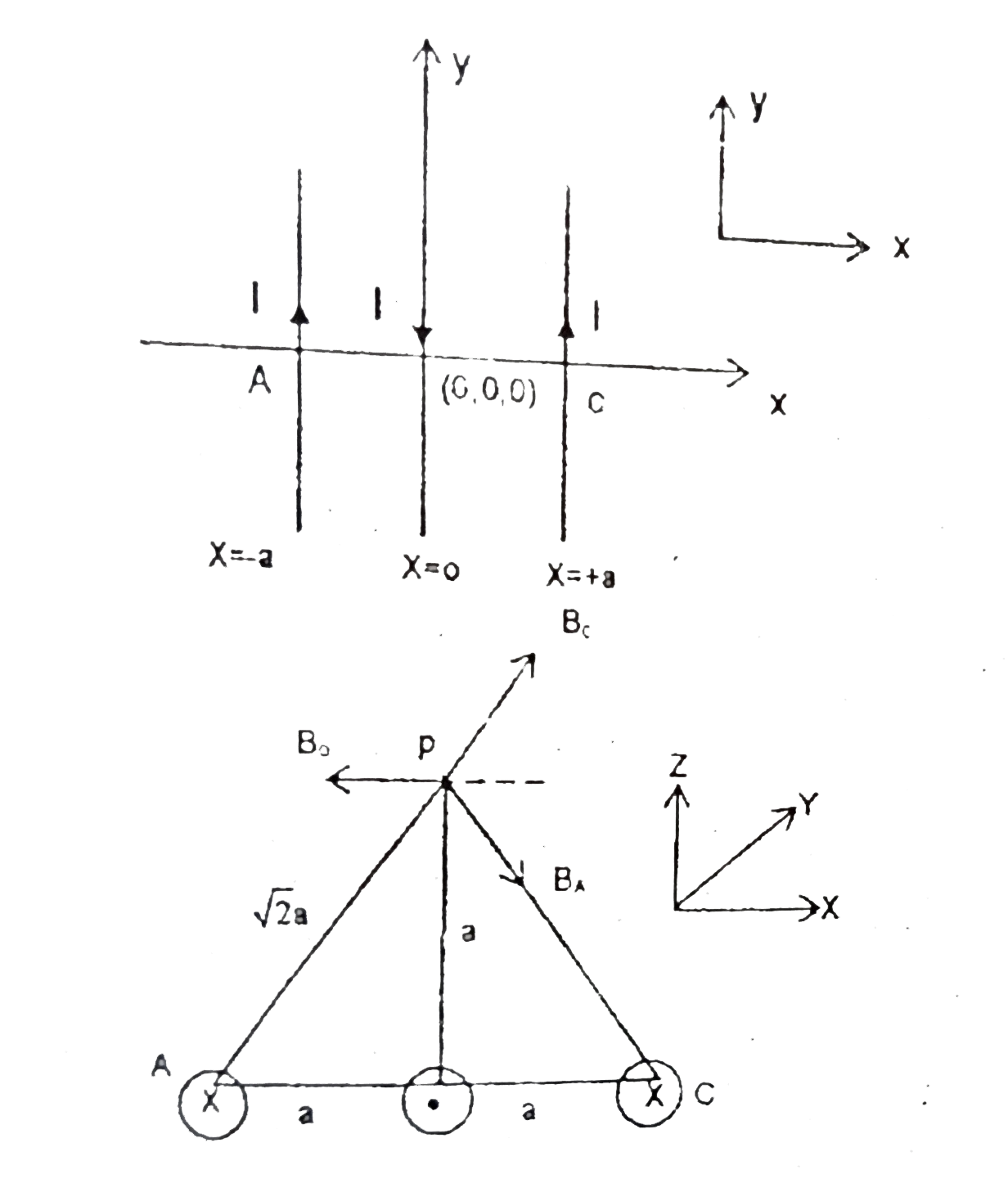
By symmetry, the net field is Zero
The net field at P(0,0,a)
→B=→BA+→B0+→Bc
=μ0I2πa√2{cos45∘ˆi+sin45∘(−ˆk)}+μ0I2πa(−ˆi)+μ0I2πa√2{cos45∘ˆi+sin45∘(ˆk)}]
=μ0I2πa√2√2ˆi+μ0I2πa(−ˆi)
=μ0I2πa[ˆi−ˆi]=0
Topper's Solved these Questions
- GMP ASSESMENTBook:FIITJEEChapter:GMP ASSESMENTExercise:Assertion & Reason
Explore 15 Videos
- GMP ASSESMENTBook:FIITJEEChapter:GMP ASSESMENTExercise:Multiple Question
Explore 58 Videos
- GMP ASSESMENTBook:FIITJEEChapter:GMP ASSESMENTExercise:Numerical Based
Explore 61 Videos
- GENERAL PHYSICSBook:FIITJEEChapter:GENERAL PHYSICSExercise:MATRIX MATCH TYPE
Explore 3 Videos
- GRAVITATIONBook:FIITJEEChapter:GRAVITATIONExercise:Numerical based Question
Explore 2 Videos
Similar Questions
Knowledge Check
Two infinitely long wires each carrying current I along the same direction are made into the geometry as shown in the figure. The magnetic field at the point P is
 Aμ0IπrBμ0Ir(1π+14)CZeroDμ0I2πr
Aμ0IπrBμ0Ir(1π+14)CZeroDμ0I2πrA long wire carrying current 'I' is bent into the shape as shown in the figure. The net magnetic field intensity at the centre 'O' is
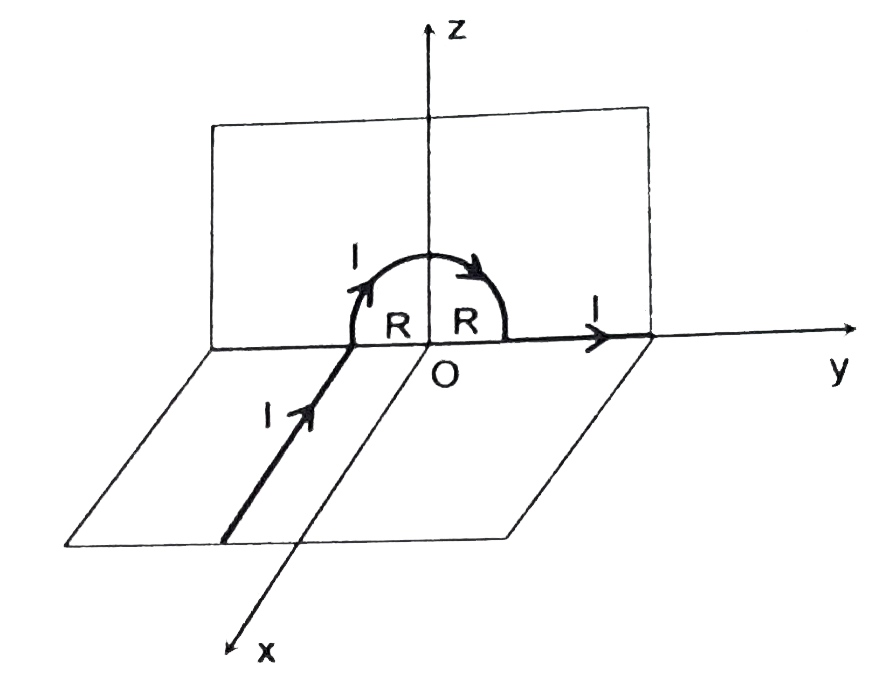 Aμ0I4πR√1+π2Bμ0I4πR√2+π2Cμ0I4πR√4+π2Dμ0I4πR√9+π2
Aμ0I4πR√1+π2Bμ0I4πR√2+π2Cμ0I4πR√4+π2Dμ0I4πR√9+π2Two thin long wires carry currents I1andI2 along x- and y-axes, respectively, as shown in Fig. Consider the points only in x-y plane.
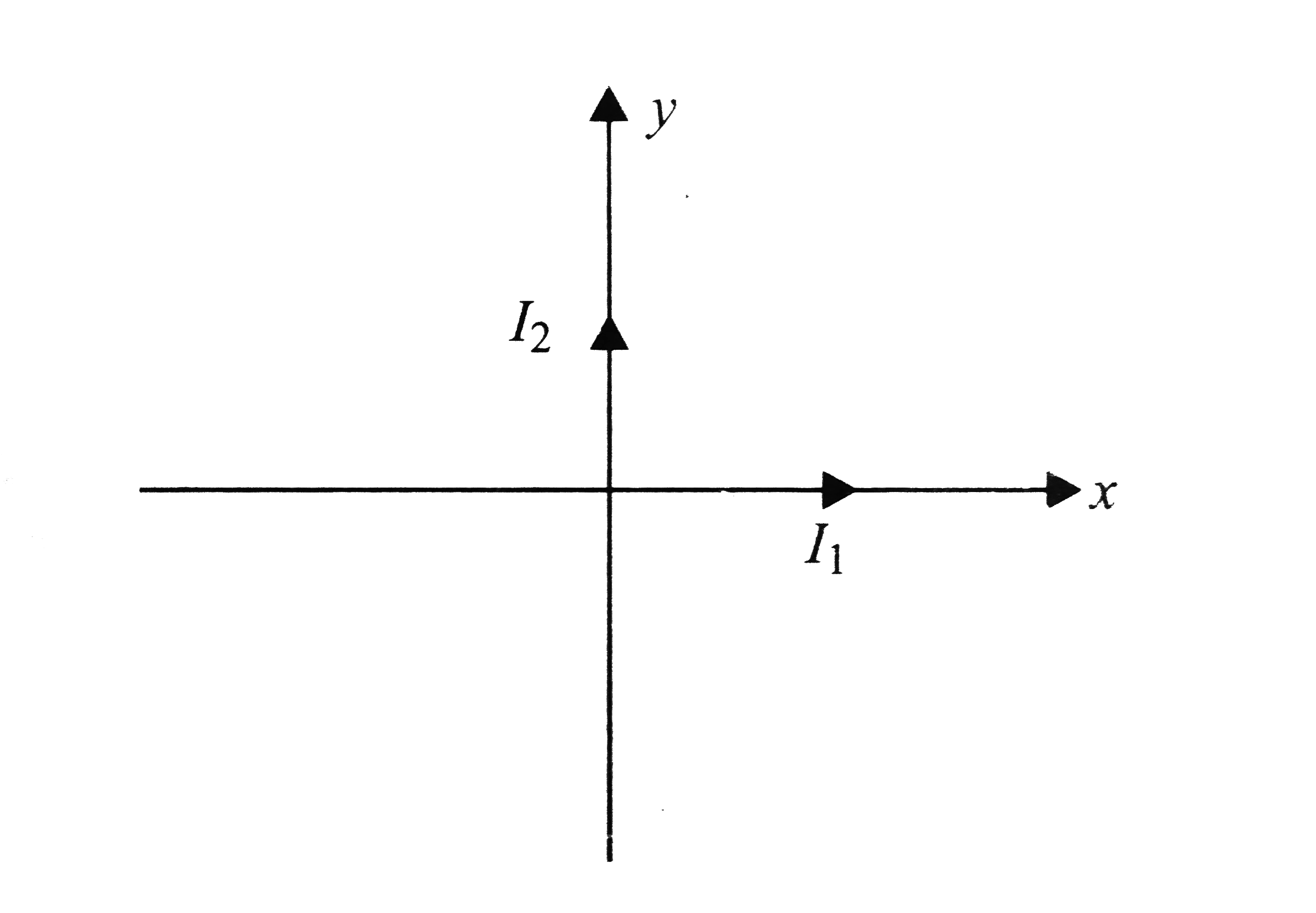 AMagnetic field is zero at last at one point in each quadrantBMagnetic field can be zero somewhere in the first quadrantCMagnetic field can be zero somewhere in the second quadrantDMagnetic field in non-zero in second quadrant
AMagnetic field is zero at last at one point in each quadrantBMagnetic field can be zero somewhere in the first quadrantCMagnetic field can be zero somewhere in the second quadrantDMagnetic field in non-zero in second quadrant
Two perpendicular infinite wires are carrying current i as shown in the figure. The magnetic field at point P is :
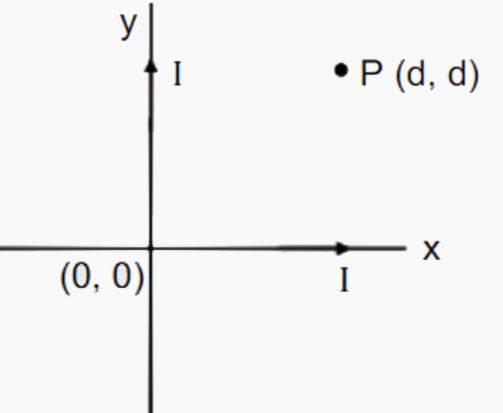
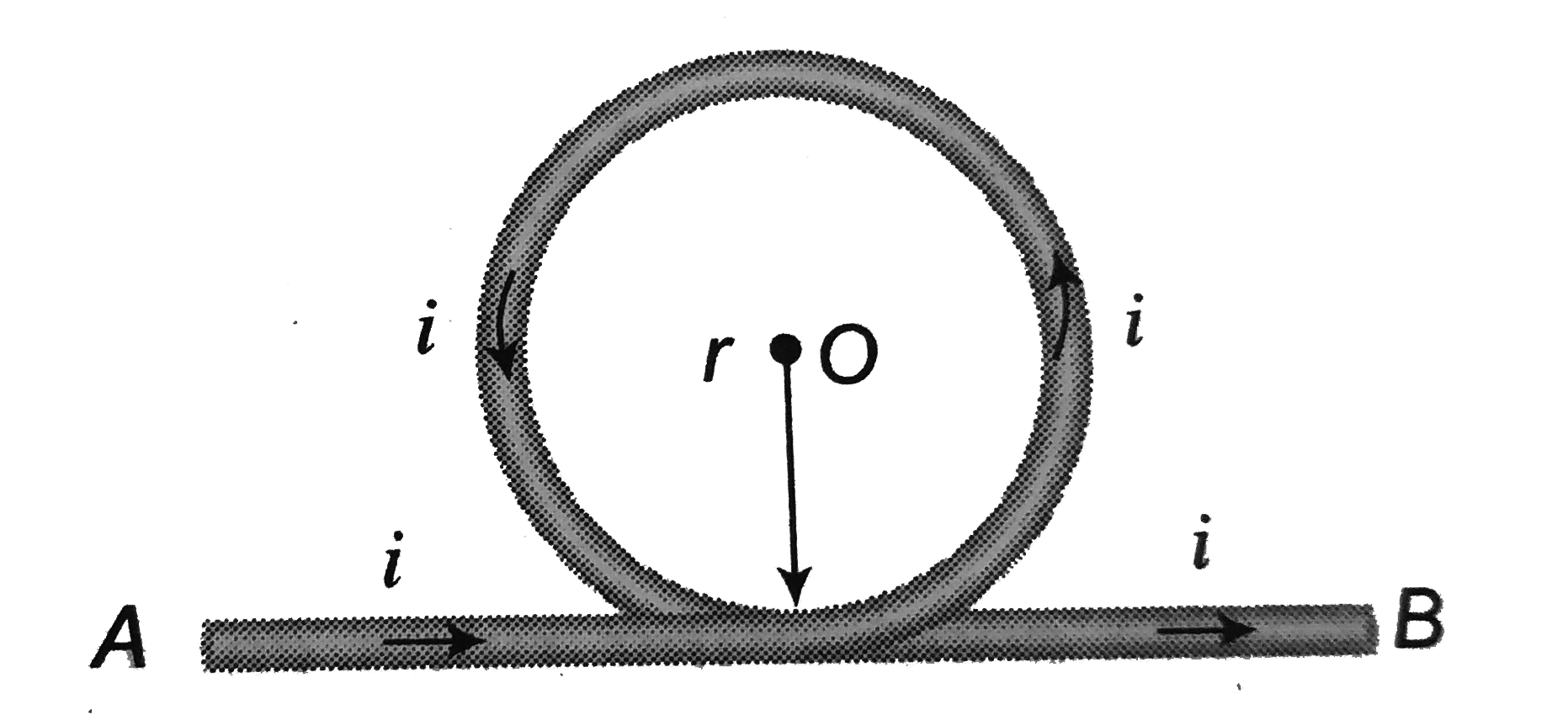
View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is
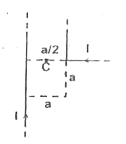
View Solutionone of the two infinitely long wires carrying current I is bent as shown in the adjacent figure. The magnetic induction at C is equal to
View SolutionTwo infinite length wires carries currents 8A and 6A respectively and placed along X and Y-axis. Magnetic field at a point P(0,0,d)m will be
View SolutionTwo infinite length wires carry currents 8A and 6A and are placed along X-asis and Y-axis respectively. Magnetic field at a point P(0, 0, d)m will be
View Solution