A long, cylindrical wire of radius b carries a current i distributed uniformly over its cross section. Find the magnitude of the magnetic field at a point inside the wire at a distance a from the axis.
a=R+r2
a=√Rr
a=Rr/R+r
a=R2/r
Applying Ampere's circuital law,
B2πr=μ0Iπr2πa2 for r<a
and B2πR=μ0I for R>a
Taking the ratio
rR=r2a2
∴a=√Rr
Topper's Solved these Questions
- GMP ASSESMENTBook:FIITJEEChapter:GMP ASSESMENTExercise:Assertion & Reason
Explore 15 Videos
- GMP ASSESMENTBook:FIITJEEChapter:GMP ASSESMENTExercise:Multiple Question
Explore 58 Videos
- GMP ASSESMENTBook:FIITJEEChapter:GMP ASSESMENTExercise:Numerical Based
Explore 61 Videos
- GENERAL PHYSICSBook:FIITJEEChapter:GENERAL PHYSICSExercise:MATRIX MATCH TYPE
Explore 3 Videos
- GRAVITATIONBook:FIITJEEChapter:GRAVITATIONExercise:Numerical based Question
Explore 2 Videos
Similar Questions
A long, straight wire of radius R carries a current distributed uniformly over its cross section. The magnitude of the magnetic field is
View SolutionA long, cylindrical tube of inner and outer radii a and b carries a current i distributed uniformly over its cross section. Find the magnitude of the magnetic field at a point (a) just inside the tube (b) just outside the tube.
View Solution
Knowledge Check
A long cylinder of wire of radius 'a' carries a current i distributed uniformly over its cross section. If the magnetic fields at distances r<aandR>a from the axis have equal magnitude, then
Aa=R+r2Ba=√ReCa=Rr/(R+r)Da=R2/rA long straight wire of radius 10mm carries a current uniformly distributed over its cross section. The ration of magnetic fields due to the wire at distance of 5mm and 15 mm, respectively from the axis of the wire is
A34B23C13D2A cylindrical long wire of radius R carries a current I uniformly distributed over the cross sectional area of the wire. The magnetic field at a distance x from the surface inside the wire is
Aμ0I2π(R−x)Bμ0I2πxCμ0I2π(R+x)Dnone of these
A long thick conducting cylinder of radius 'R' carries a current uniformly distributed over its cross section :
View SolutionConsider a long cylindrical wire carrying current along the axis of wire. The current distributed non-uniformly on cross section. The magnetic field B inside the wire varies with distance r from the axis as B=kr4 where k is a cosntant. The current density J varies with distance r as J=crn then the value of n is (where c is another constant).
View SolutionA hollow cylindrical conductor of inner radius a and outer radius b carries a current I uniformly spread over its cross-section. Find the magnetic field induction at a point inside the body of the conductor at a distance r [where a<r<b] from the axis of the cylinder.
View SolutionA long straight solid metal rod of radius 4cm carries a current 2A, uniformly distributed over its circular cross-section. Find the magnetic field induction at a distance 3cm from the axis of the wire.
View SolutionA very long cylindrical wire is carrying a current I0 distriuted uniformly over its cross-section area. O is the centre of the cross-section of the wire and the direction of current in into the plane of the figure. The value ∫BA→B.→dl along the path AB (from A to B ) is
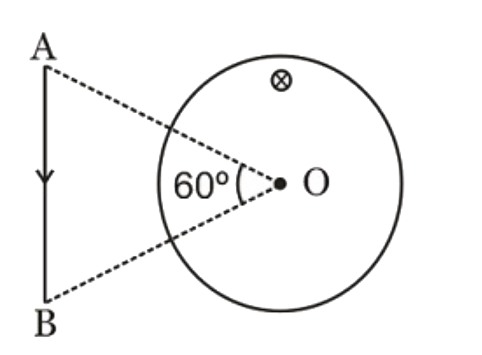
View Solution

