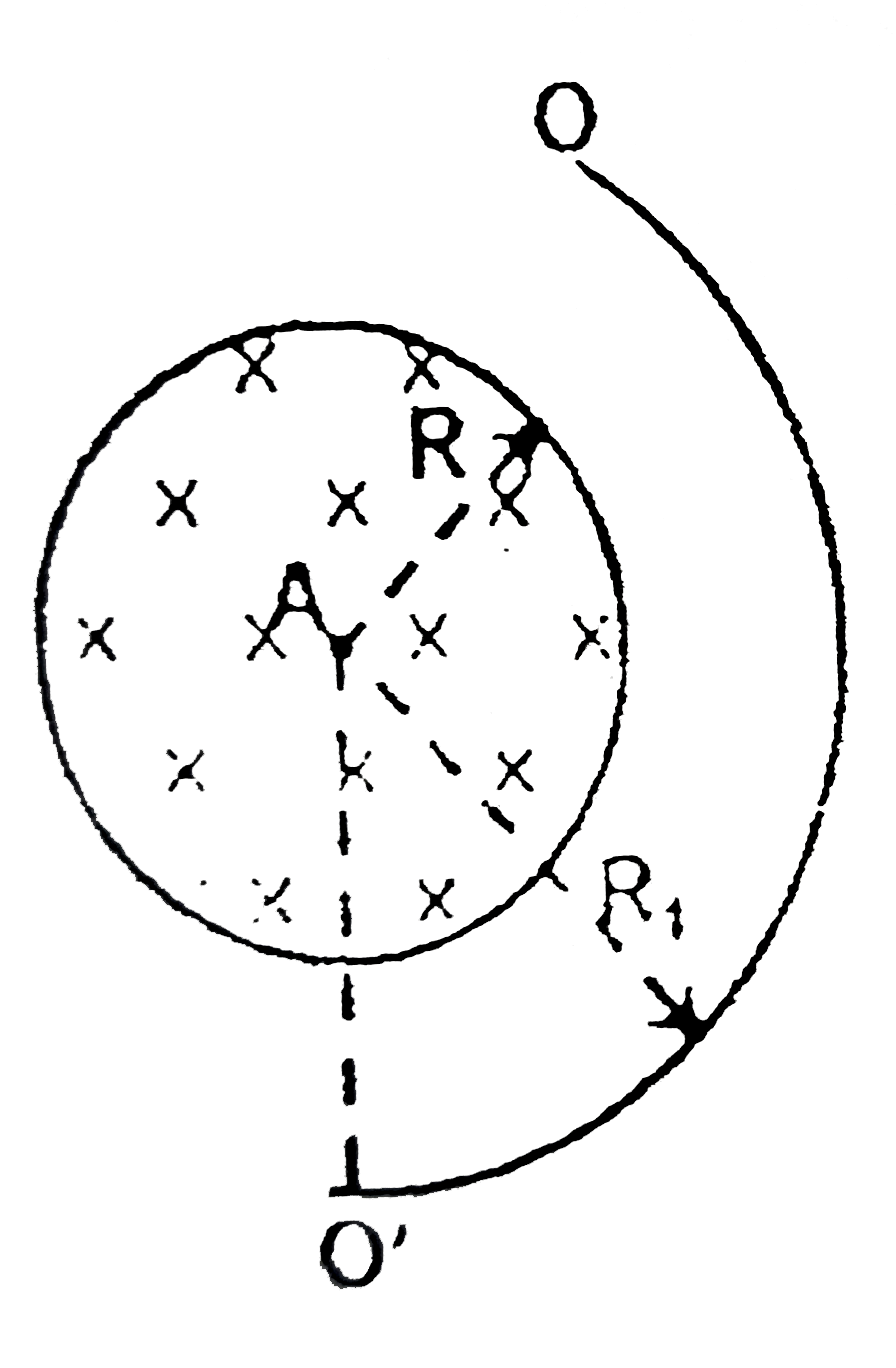
There is a uniform magnetic field B in a circular region of radius R as shown in Fig. 3.149 whose magnitude changes at the rate of dB/dt. The emf circular concentric conducting arc of radius R1 having an angle θ as shown (−OAO'=θ) is

θ2πR21dBdt
θ2R2dBdt
θ2πR2dBdt
none of these
Required emf =πR2dBDt⋅θ2π
∴E=R22R1(dBdt)
emf=θ2πR22R1(dBDt)2πR1=θ2R2(dBdt)
Related Playlists
- BOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Assertion & Reason15videos
GMP ASSESMENT
- BOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Multiple Question58videos
GMP ASSESMENT
- BOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Numerical Based61videos
GMP ASSESMENT
- BOOK - FIITJEECHAPTER - GENERAL PHYSICSEXERCISE - MATRIX MATCH TYPE3videos
GENERAL PHYSICS
- BOOK - FIITJEECHAPTER - GRAVITATIONEXERCISE - Numerical based Question2videos
GRAVITATION
Similar Questions
Magnetic field in cylindrical region of radius R in inward direction is as shown in figure.
 View Solution
View SolutionA uniform magnetic field B exists in a circular region of radius R. the field is perpendicular to the plane and is increasing at a constant rate of dBdt=α. There is a straight conducing rod AB of length 2R. Find the emf induced in the rod when it is placed as shown in figure (a) & (b). Point C is midpoint of the rod in figure (b)
 View Solution
View SolutionThe magnetic field perpendicular to the plane of a conducting ring of radius r changes at the rate.dBdt . Then
View SolutionA uniform magnetic field is applied in a circular region of radius R as shown in the given figure. A charged particle of charge q and mass m enters with a velocity from point P along the line that is making an angle with the line segment OP, in the region of magnetic field.
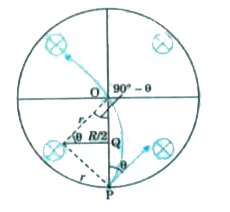
The charged particle is found to pass through the centre of the circular region. Find the angle θ.
Given : B=1T,R=10cm,m=6×10−3kg,q=6×10−2C,v=1/√3.View SolutionThere is a uniform magnetic field (B) perpendicular to the plane of the figure in a circular region of radius a centred at O. ABCD is a conducing loop in the plane of the figure with its arms BC and DA along two radial lines from O having an angle θ between them. AB is circular arc of radius OB = d centred at O. CD is also a circular arc of radius OC=b centred at O. The magnetic field is changed at a rate dBdt.
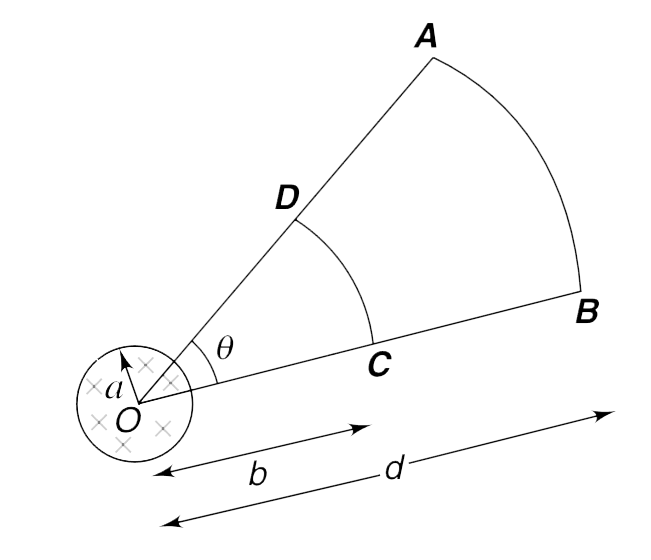
(a) The emf induced in the loop ABCD.
(b) Find emf induced in arc AB.View SolutionA particle of charge q and mass m is projected with a velocity v0 toward a circular region having uniform magnetic field B perpendicular and into the plane of paper from point P as shown in Fig. 1.136. R is the radius and O is the center of the circular region. If the line OP makes an angle θ with the direction of v0 then the value of v0 so that particle passes through O is
 View Solution
View SolutionThe magnetic field perpendicular to the plane of a conducting ring of radius r change ate the rate dBdt
View SolutionIn a very long solenoid of radius R, if the magnetic field chabges at the rate of dB/dt.AB=BC
The induced emf for the trianglar circuit ABC shown in Fig. 3.196 is
 View Solution
View SolutionA straight wire carrying a current of 5 A is bent into a semicircular arc of radius 2 cm as shown in the fig. Find the magnitude and direction of the magnetic field at the centre of the arc.
 View Solution
View SolutionA uniform magnetic field is restricted within a region of radius r. The magnetic field changes with time at a rate dBdt. Loop 1 of radius R > r encloses the region r and loop 2 of radius R is outside the region of magnetic field as shown in figure. Then, the emf generated is
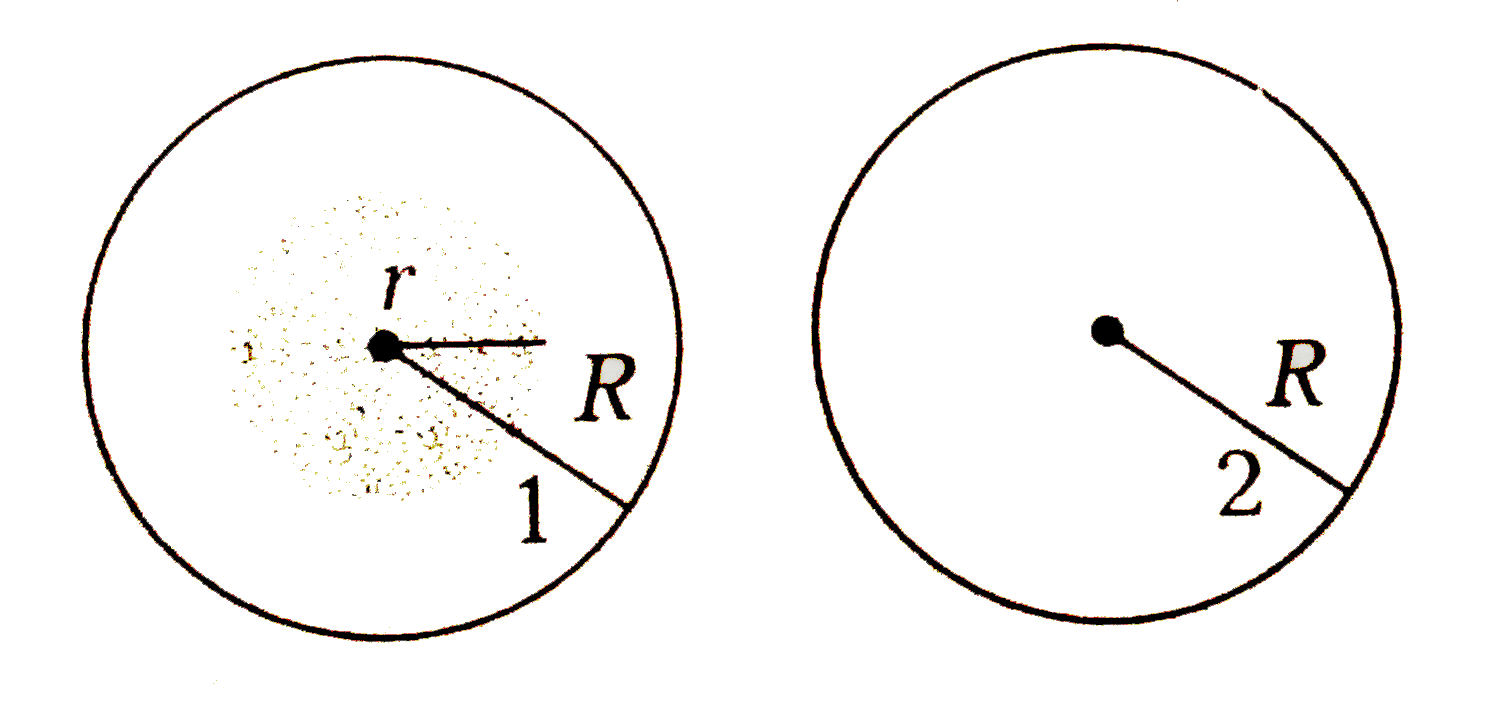 View Solution
View Solution


