A long straight wire along the z-axis carries a current I in the negative z-direction. The magnetic vector field B at a point having coordinate on the plane is:
The correct Answer is:A
Magnetic field at P is B. Perpendicular to OP in the direction shown in figure.
So Here and
(as

Similar Questions
(a) Find the magnetic field at the point O if the wire carrying a current i has the shape shown. The radius of the current part of the wire is R, the linear parts of the wire are very long.
(i)
(ii)
(iii)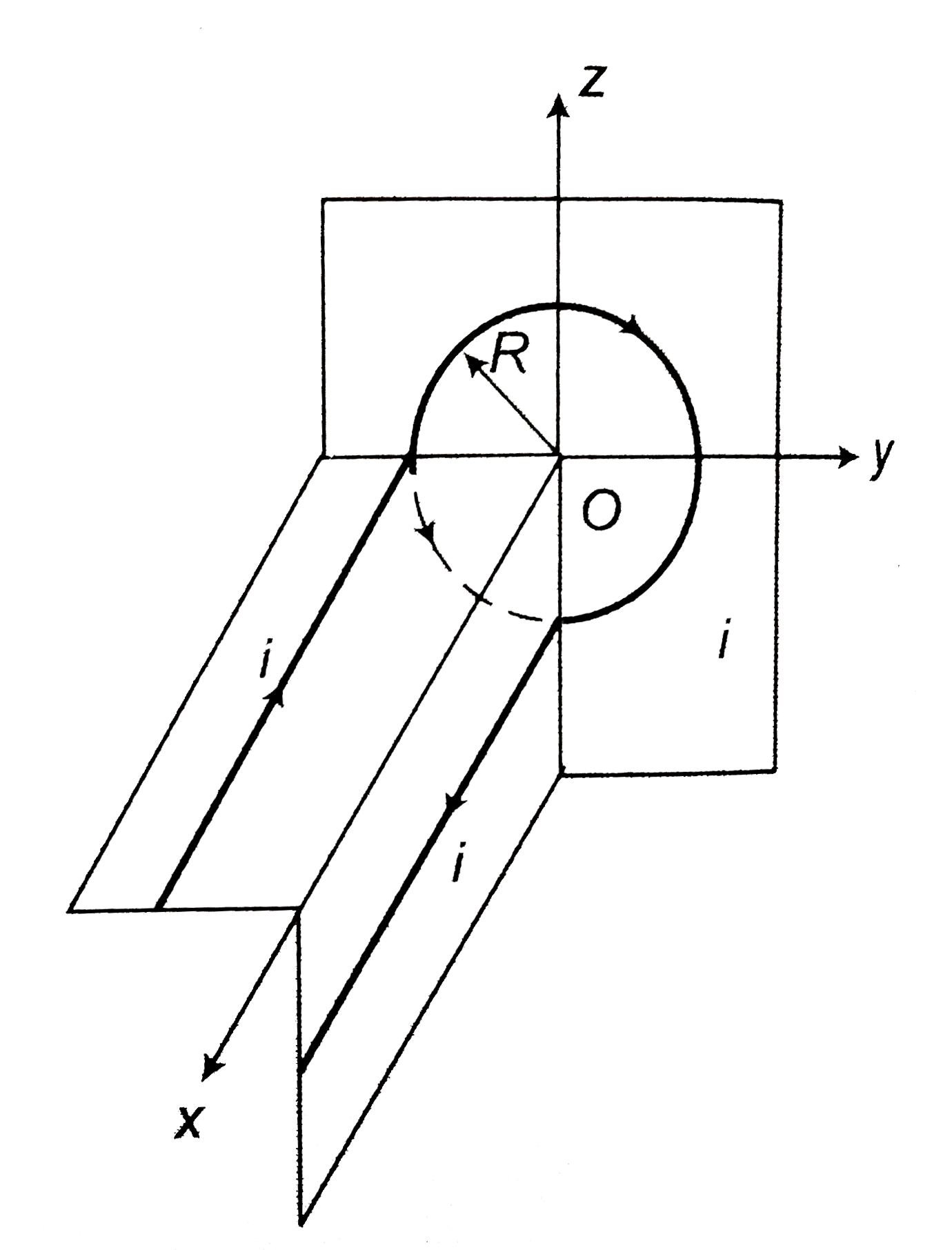
(b) A long straight wire along the z-axis carriers a current i in negative z-direction. Find magnetic field in vector from at a point having co-ordinates (x,y) on z=0 plane.
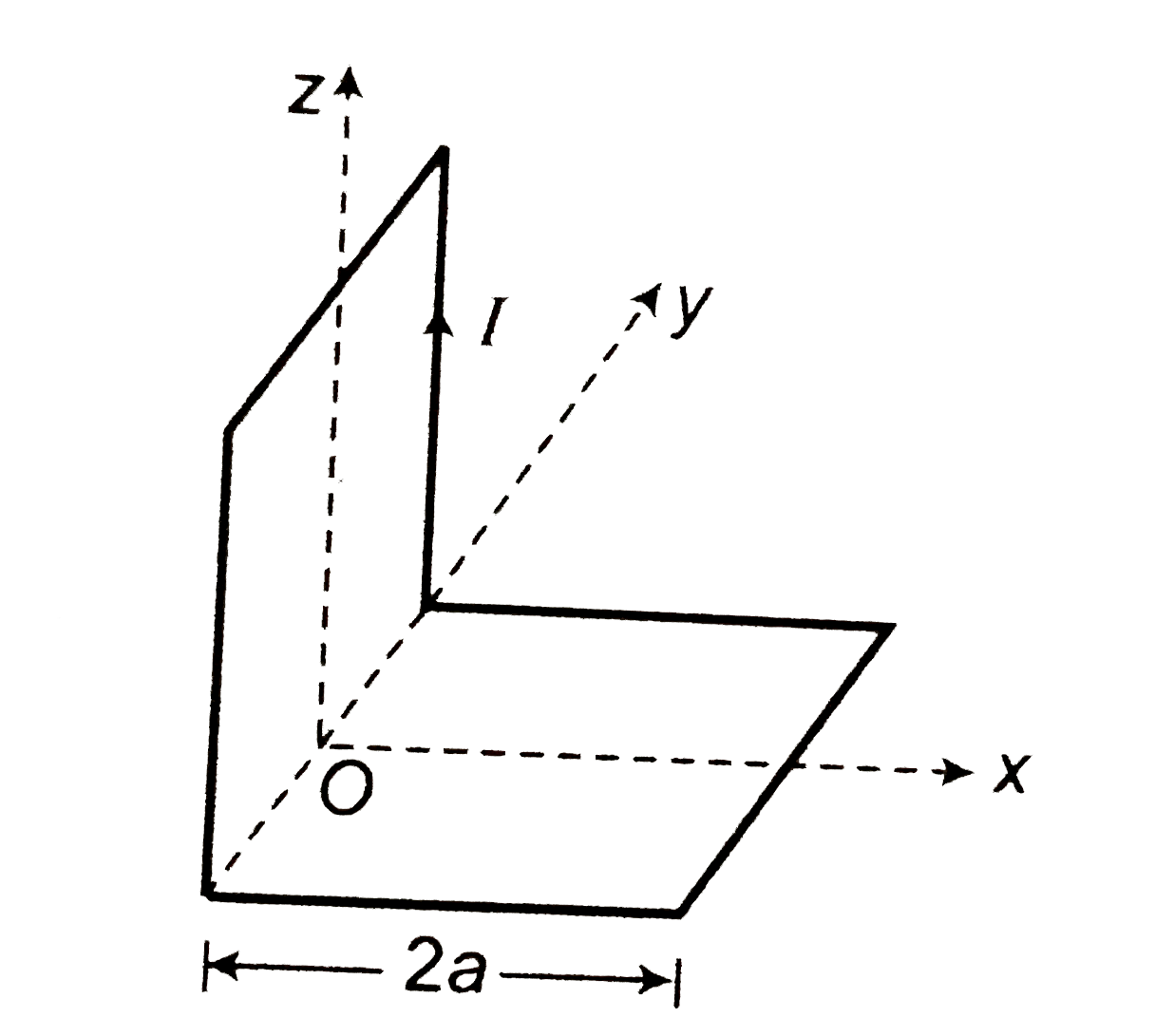
(c) A non-coplaner loop of conducting wire carrying a current I is placed as shown in the figure. Each of the straight sections of the loop of length 2a. find unit vector along magnetic field magnetic filed at the point P(a,0,a).
View SolutionA long, straight wire lies along the y-axis and carries a current I=8A in the y-direction (as shown in Fig) In addition to the magnetic field due to the current in the wire, a uniform magnetic field →B0 with magnitude 1.50×10−6T is in the +x direction. What is the total field (magnitude and direction ) at following points in the plane?
(a)x=0,z=1.00m
(b) x=1.00m,z=0
(c) x=0,z=−0.25m

View Solution
Knowledge Check
A long straight wire along the z-axis carries a current I in the negative z-direction. The magnetic vector field →B at a point having coordinnates (x, y) in the z = 0 plane is
Aμ0I(yˆi−xˆj)2π(x2+y2)Bμ0I(xˆi+yˆj)2π(x2+y2)Cμ0I(xˆj−yˆi)2π(x2+y2)Dμ0I(xˆi−yˆj)2π(x2+y2)A long straight wire along the z-axis carries a current I in the negative z-direction. The magnetic vector field →B at a point having coordinnates (x, y) in the z = 0 plane is
Aμ0I(yˆi−xˆj)2π(x2+Y2)Bμ0I(xˆi+yˆj)2π(x2+Y2)Cμ0I(xˆj−yˆi)2π(x2+Y2)Dμ0I(xˆi−yˆj)2π(x2+Y2)A long straight wire along the z−aξs carries a current I in the negative z−direction . The magnetic vector field →B at a point having coordinates (x,y) in the Z=0 plane is
Aμ0I(yˆi)−xˆj2π(x2+y2)Bμ0I(xˆi)+yˆj2π(x2+y2)Cμ0I(xˆj)−yˆi2π(x2+y2)Dμ0I(yxˆi)−yˆj2π(x2+y2)
A long straight wire carries a current of 35A. What is the magnetic of the field →B at a point 20cm from the wire?
View SolutionAn infinitely long, noc-conducting cylidner of radius R lies along the z-axis. Five long, conducting wires are parallel to the cylinder and spaced equally on the upperhalf of its surface. Each wire carries a current I in the opposite z-direction. Find the magnetic field on the z-axis. opposite z-direction. Find the magnetic field on the z-axis.
View SolutionA long, straight wire carries a current along the z-axis. One can find two points in the x-y plane such that
View SolutionA long straight wire in the horizontal plane carries as curret of 75 A in north to south direction, magnitude and direction of field B at a point 3 m east of the wire is
View SolutionA very long straight wire of radius 'r carries current 'I'. Intensity of magnetic field 'B' at a point, lying at a perpendicular distance 'a' from the axis is ∝ ___________
View Solution
