Consider a block of conducting material of resistivity 'ρ' shown in the figure. Current 'I' enters at 'A' and leaves from 'D'. We apply superposition principle to find voltage ΔV developed between 'B' and 'C'. The calculation is done in the following steps:
(i) Take current 'I' entering from 'A' and assume it to spread over a hemispherical surface in the block.
(ii) Calculate field E(r) at distance 'r' from A by using Ohm's law E=ρj, where j is the current per unit area at 'r'.
(iii) From the 'r' dependence of E(r), obtain the potential V(r) at r.
(iv) Repeat (i), (ii) and (iii) for current 'I' leaving 'D' and superpose results for 'A' and 'D'.
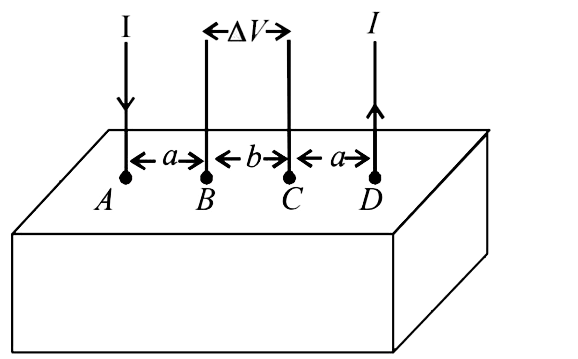
For current entering at A, the electric field at a distance 'r'
ρI4πr2
ρI8πr2
ρIr2
ρI2πr2
The correct Answer is:D
Step by step video, text & image solution for Consider a block of conducting material of resistivity 'rho' shown in the figure. Current 'I' enters at 'A' and leaves from 'D'. We apply superposition principle to find voltage DeltaV developed between 'B' and 'C'. The calculation is done in the following steps: (i) Take current 'I' entering from 'A' and assume it to spread over a hemispherical surface in the block. (ii) Calculate field E(r) at distance 'r' from A by using Ohm's law E = rhoj, where j is the current per unit area at 'r'. (iii) From the 'r' dependence of E(r), obtain the potential V(r) at r. (iv) Repeat (i), (ii) and (iii) for current 'I' leaving 'D' and superpose results for 'A' and 'D'. For current entering at A, the electric field at a distance 'r' by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
As shown in the figure 'rho' Consider a block of resistive conductive material. Section 'I' flows through 'A' and gets expelled from 'D'. We originated between 'B' and 'C' Delta V The principle of imputation is used to find the voltage. The calculation is done in the following terms. : (i) Assume Section 'I' entering from A and assume that it spreads above the semicircular surface in the block. (ii) Ohm's law E=rho j Calculate the electric field E (r) at the distance from A to r using the area j per unit area on 'r'. (iii) The dependence of E (r) on r gives the potential V (r) at r. (iv) Repeat (i), (ii) and (iii) for Section I issued from D and install the results for A and D. For the current entering from A, the electric field at the distance 'r' from A is -
View SolutionAs shown in the figure 'rho' Consider a block of resistive conductive material. Section 'I' flows through 'A' and gets expelled from 'D'. We originated between 'B' and 'C' Delta V The principle of imputation is used to find the voltage. The calculation is done in the following terms. : (i) Assume Section 'I' entering from A and assume that it spreads above the semicircular surface in the block. (ii) Ohm's law E=rho j Calculate the electric field E (r) at the distance from A to r using the area j per unit area on 'r'. (iii) The dependence of E (r) on r gives the potential V (r) at r. (iv) Repeat (i), (ii) and (iii) for Section I issued from D and install the results for A and D. Measured between B and C Delta V is -
View SolutionFrom the given between current I and voltage V shown in figure , indentify the portion corresponding to negative resistance
View SolutionCurrent I enters at A in a square loop of uniform resistance and leaves at B. The ratio of magnetic field at E, the centre of square, due to segment AB to that due to DC is

View SolutionConsider a block of conducting material of resistivity 'ρ' shown in the figure. Current 'I' enters at 'A' and leaves from 'D'. We apply superposition principle to find voltage ΔV developed between 'B' and 'C'. The calculation is done in the following steps:
(i) Take current 'I' entering from 'A' and assume it to spread over a hemispherical surface in the block.
(ii) Calculate field E(r) at distance 'r' from A by using Ohm's law E=ρj, where j is the current per unit area at 'r'.
(iii) From the 'r' dependence of E(r), obtain the potential V(r) at r.
(iv) Repeat (i), (ii) and (iii) for current 'I' leaving 'D' and superpose results for 'A' and 'D'.
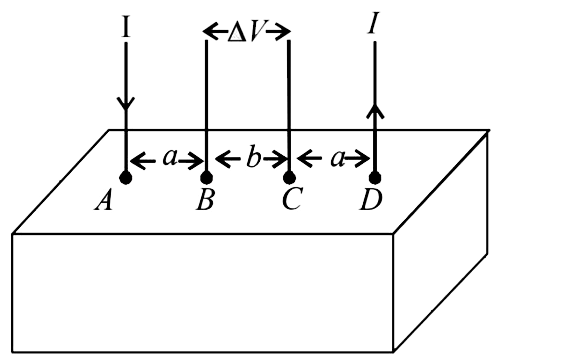
Delta V measured between B and C is
View SolutionA small block slides down from the top of hemisphere of radius R = 3 m as shown in the figure. The height 'h' at which the block will lose contact with the surface of the sphere is __________ m. (Assume there is no friction between the block and the hemisphere)
View SolutionConsider a block of conducting material of resistivity p shown in the figure. Current l enters at A and leaves from D. We apply superposition principle to find voltage DeltaV developed between B and C. The calculation is done in the following steps : (a) Take current I entering from A and assume it to spread over a hemispherical surface in the block. (b) Calculate field E (r) at distance r from A by using Ohm's law E = pj, where j is the current per unit area at r. (c) From the r dependence ofE (r), obtain the potential V (r) at r. (d) Repeat (I), (ii) and (iii) for current l leaving D and superpose results for A and D. DeltaV measured between B and C is :
View SolutionConsider a block of conducting material of resistivity p shown in the figure. Current l enters at A and leaves from D. We apply superposition principle to find voltage ΔV developed between B and C.
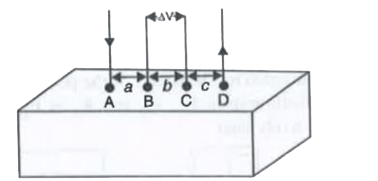
The calculation is done in the following steps :
(a) Take current I entering from A and assume it to spread over a hemispherical surface in the block.
(b) Calculate field E (r) at distance r from A by using Ohm's law E = pj, where j is the current per unit area at r.
(c) From the r dependence ofE (r), obtain the potential V (r) at r.
(d) Repeat (I), (ii) and (iii) for current l leaving D and superpose results for A and D.
For current entering at A, the electric field at a distance r from A is
View Solution
