पैरा 4
चित्र II.75 में दिखाया गया प्रतिरोधकता वाला चालक पदार्थ का एक गुटका लें। धारा , बिन्दु A से प्रवेश करती है और D से बाहर निकलती है। हम अध्यारोपण का नियम लगाकर B और C के बीच पैदा हुई वोल्टता निकालते हैं। यह इन चरणों में किया जाता है :
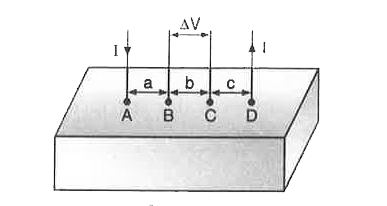
(i ) मान लें कि धारा, I, बिन्दु A से प्रवेश करती हैं और गुटके में एक गोलार्ध पृष्ठ पर फैली हुई है।
(ii) A से r दुरी पर क्षेत्र E(r) ओम का नियम प्रयुक्त करते हुए निकालें जहाँ j, r दूरी पर प्रति यूनिट क्षेत्रफल धारा है। की पर निर्भरता से पर विभव V (r) निकालें।
(iv) D से निकल रही धारा I के लिए (i), (ii) और (iii) को दोहराएँ औरA और D के लिए परिणामों का अध्यारोपण करें।
B और C के बीच मापा गया है
The correct Answer is:C
बिन्दु A से r दूरी पर विद्युत क्षेत्र
( क्योंकि व्यासार्ध वाले गोलार्ध का पृष्ठीय क्षेत्रफल है )
क्योंकि , इसलिए
( B के लिए और के लिए )
या
Topper's Solved these Questions
- विद्युत परिपथ , विद्युत ऊर्जा और शक्ति Book:GRB PUBLICATION HINDIChapter:विद्युत परिपथ , विद्युत ऊर्जा और शक्ति Exercise:प्रतियोगिता सामग्री ( कॉलम मिलाना )
Explore 4 Videos
- विद्युत परिपथ , विद्युत ऊर्जा और शक्ति Book:GRB PUBLICATION HINDIChapter:विद्युत परिपथ , विद्युत ऊर्जा और शक्ति Exercise:प्रतियोगिता सामग्री ( कथन-कारण-आधारित प्रश्न )
Explore 12 Videos
- विद्युत परिपथ , विद्युत ऊर्जा और शक्ति Book:GRB PUBLICATION HINDIChapter:विद्युत परिपथ , विद्युत ऊर्जा और शक्ति Exercise:NCERT पाठ्य-पुस्तक अभ्यास : उत्तरों सहित
Explore 8 Videos
- प्रत्यावर्ती धाराएँ Book:GRB PUBLICATION HINDIChapter:प्रत्यावर्ती धाराएँ Exercise:रिक्त स्थान भरना
Explore 15 Videos
- वैद्युत क्षेत्र और गाउस नियमBook:GRB PUBLICATION HINDIChapter:वैद्युत क्षेत्र और गाउस नियमExercise:NCERT पाठ्यपुस्तक अभ्यास : उत्तरो सहित
Explore 29 Videos
Similar Questions
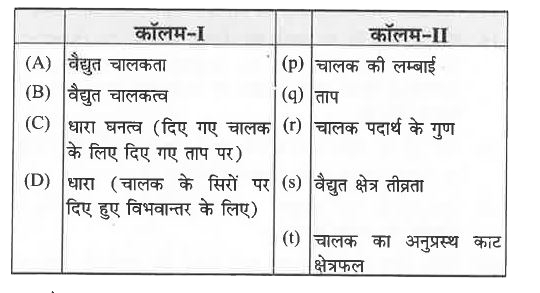
कॉलम-I में दिए गए चालकों के गुणों का कॉलम-II में दी गई राशियों से मिलान करें।
View SolutionA : बड़े शुष्क सेल का विधुत वाहक बल ज्यादा होता है।
R : शुष्क सेल का विधुत वाहक बल, इसके साइज़ पर निर्भर करता है
View Solutionएक कार की संचायक बैटरी का विधुत वाहक बल10 V है। यदि बैटरी का आन्तरिक प्रतिरोध 0.4Ω हो, तो बैटरी से अधिकतम कितनी धारा ली जा सकती है ?
View Solutionएक शुद्ध प्रेरकत्व में क्षयित हुई औसत शक्ति.........।
View Solutionहवा में एक दूसरे से 30 cm दूर रने 2×10−7C और 3×10−7C आवेश वाले दो छोटे आवेशित गोलों के बीच बल ज्ञात करें।
View Solutionएक सरल रेखा बिन्दु (-1,5) से होकर जाती है और रेखा द्वारा अक्षो के बीच काटे हुए भाग को यह बिन्दु 3:2 के अनुपात में विभाजित करता है। रेखा का समीकरण ज्ञात कीजिए|
View Solutionयदि एक वक्र बिंदु (1, -2) से होकर जाता है तथा इस पर किसी बिंदु (x, y) पर स्पर्श रेखा का ढाल (slope) x2−2yx है, तो यह वक्र निम्न में से किस बिंदु से होकर जाता है ?
View Solutionनिम्नलिखित में से कौन-सी संख्या 45 और 95 के बीच में नहीं है :
View Solutionनिम्न में से कौन-सा कथन सत्य हैं ?
"tan A का मान सदैव-1 और 1 के बीच होता है।"
View Solutionनिम्न में से कौन-सा कथन सत्य हैं ?
"sec A का मान-1 और 1 के बीच में होता है
View Solutionनिम्नलिखित में से कौन-सा उत्तर सही है? I. अनुस्वार पूर्ण अनुनासिक ध्वनि है। II. वर्ग का पंचमाक्षर अनुनासिक होता है। III. अनुनासिक के उच्चारण के दौरान नाक से बहुत कम साँस निकलती है और मुँह से अधिक।
View Solutionपदार्थ A और B के बीच अभिक्रिया को निम्न प्रकार दर्शाया गया है
A+B−→C इस अभिक्रिया की दर से निम्न प्रेक्षणों को प्राप्त किया जाता है

View Solution5 बार और 300K पर एक आदर्श एक्परमाणविक गैस के दो मोल के 1 बार के ब्रह्म डाब तक अनुत्क्रमणीय रूप से प्रसारित किया जाता है गैस दवरा किया गया कार्य xR (बार लीटर में ) है x का मान है
View Solutionरुद्धोष्म और समतापीय स्थितियों के तहत एक आदर्श गैस का उत्क्रमणीय प्रसार चित्र में दिखाया गया है | निम्नलिखित में से कौन सा कथन अशुद्ध है
View Solutionएक आदर्श गैस के दस मोलों को एक बंद पात्र में भरा जाता है । पात्र में बेलन और पिस्टन के प्रकार की व्यवस्था है और 0.821 atm पर गैस का दाब स्थिर रहता है। निम्नलिखित में से कौन सा आलेख logV और logT के परिवर्तन का सही निरूपण करता है? (V= आयतन(लीटर में) और T= ताप (केलिवन में)
View Solutionमैग्नीशियम के निष्कर्षण धातुकर्म में निम्नलिखित में से किस प्रक्रम का उपयोग किया जाता है?
View Solution