A point charge Q is located on the axis of disc of a radius R at a distance a from the plane of the disc . If one fourth (1/4th) of the flus from the charge passes through the disc, then find the relation between a &R.
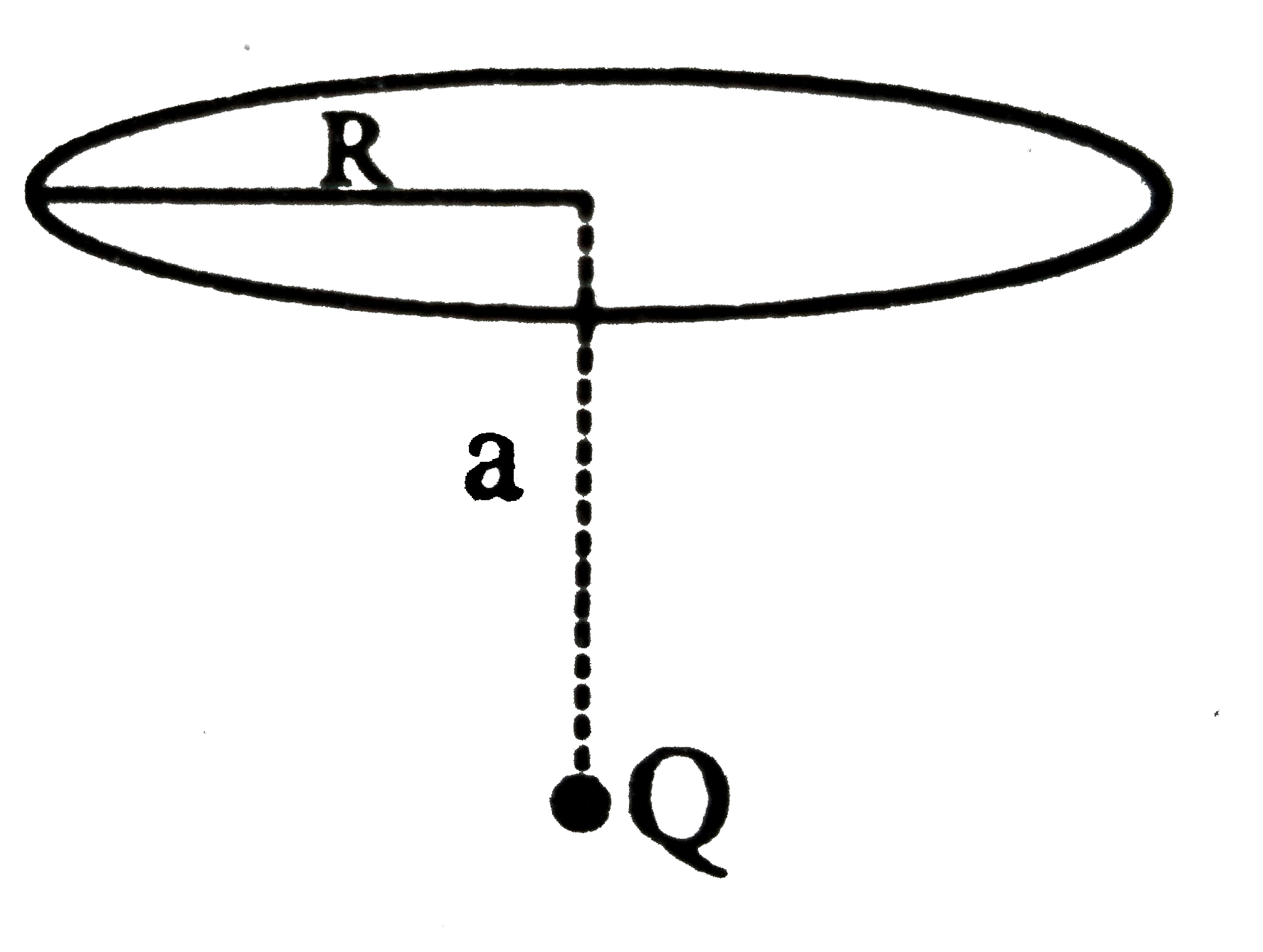 .
.
The correct Answer is:a=R√3
Flux through ring dϕ=EdAcosθ
dϕE=14π∈0Q(a2=x2).2πxdx.a√a2+x2

ϕE=14∈0Qa∫R02xdx(a2+x2)3/2 ….(1)
Put a2+x2=t
From (1) and (2)
ϕE=14ϕ0Qa∫R0dtt3/2=Qa4∈0[−2√t]r0=Qa4∈0[−2√a∘+R2]R0.
ϕE=QWa2∈0[1a−1√a2+r2=nQ2∈0(1−a√a2+R2)
ϕE=Q2∈0(1−a√R2+a2)=ϕtoal2(1−a√R2+a2)
14=12(1−na√R2+a2)
12=1−a√R2+a2⇒a√R2+a2=12
4a2=R2+a2⇒a=R√3 .
Similar Questions
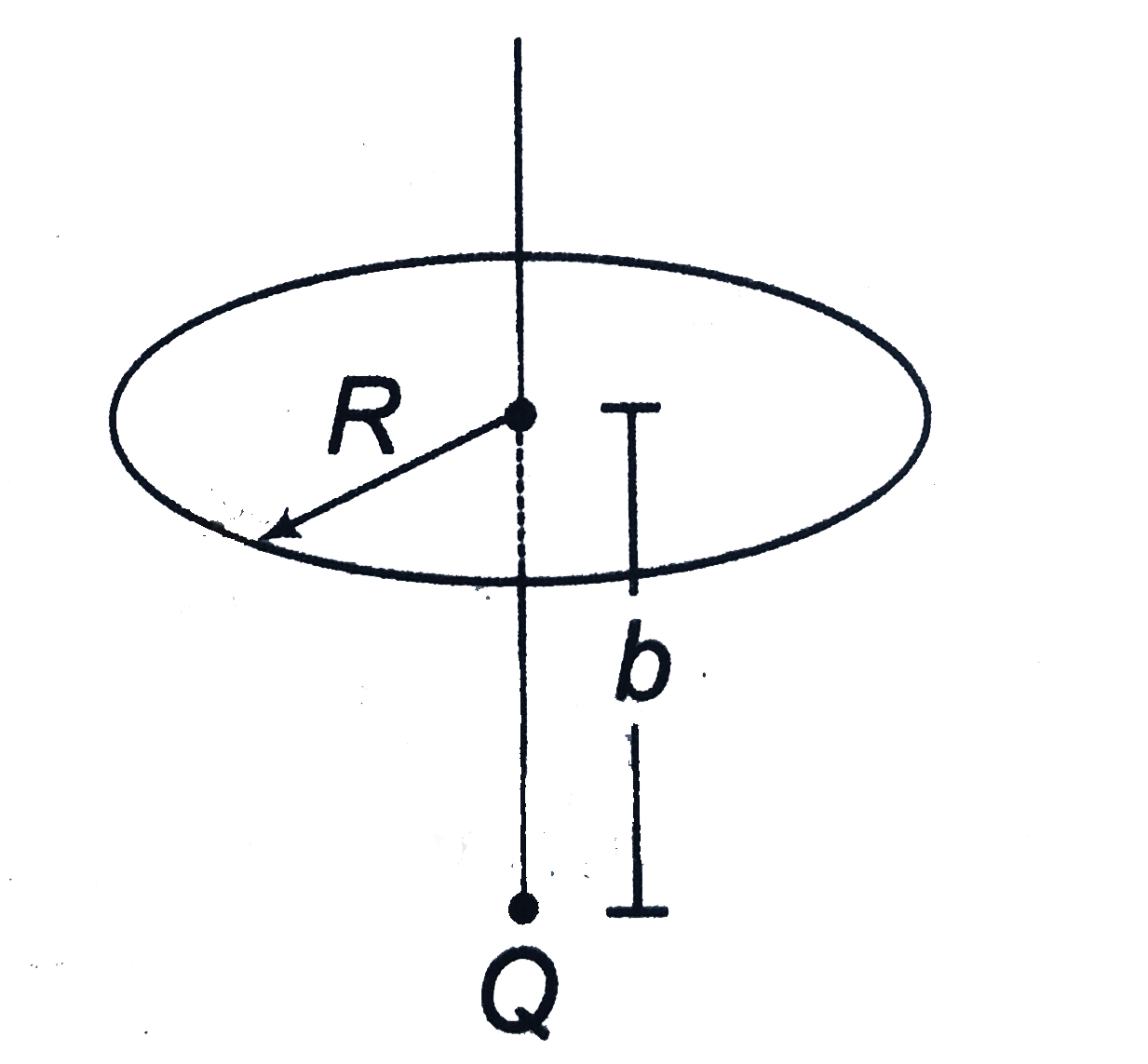
A point charge Q is located on the axis of a disk of radius R at a distance b from the plane of the disk. Show that if one-fourth of the electric flux from the charge passes through the disk, then R=√3b.

View SolutionA point charge Q is located on the axis of a disc of radius R at a distance b from the plane of the disc (figure). Show that if one-fourth of the electric flux from the charge passes through the disc, then R=√3b.
View Solution
Knowledge Check
A point charge placed on the axis of a uniformly charged disc experiences a force f due to the disc. If the charge density on the disc sigam is, the electric flux through the disc, due to the point charge will be
A2πfσBf2πσCf2σDfσA position charge q is placed at a distance of 4R above the centre of a disc of radius R. The magnitude of flux through the disc is ϕ. Now a hemispherical shell of radius R is placed over the disc such that it forms a closed surface. The flux through the curved surface (taking direction of area vector along outward normal as positive), is -
 AZeroBϕC−ϕD2ϕ
AZeroBϕC−ϕD2ϕA small hole is made in a disc of mass M and radius R at a distance R/4 from centre. The disc is supported on a horizontal peg through this hole. The moment of inertia of the disc about horizontal peg is
AMR29B516MR2C916MR2D54MR2
A point charge q is located on the axis of a disc of radius R at a distance b from the plane of the disc as shown in figure 1.295 What should be the radius of the disc if one fourth of the total electric flux form the charge passes through the disc.

View SolutionA point charge q is placed at a distance d form the center of circular disc of radius R. Find electric flux through the disc due to that charge
View SolutionCalculate potential on the axis of a disc of radius R due to a charge Q uniformly distributed on its surface.
View SolutionA point charge Q is placed at the centre of circular disc of radius r . Calculate the electric flux associated with circular disc.
View SolutionA charge q is placed at the some distance along the axis of a uniformly charged disc of surface charge density σ. The flux due to the charge q through the disc is ϕ. The electric force on charge q exerted by the disc is
View Solution

