Calculate potential on the axis of a disc of radius R due to a charge Q uniformly distributed on its surface.
When a charge Q is distributed uniformly on the surface of a circular disc of radius R, surface charge density
σ=QπR2 …(i)
Consider a small element of the circuit disc in the form of a circular strip of radius r and thickness/width dr, Fig 39,
= Area of this element, q=σrdr
Charge on this element, q=σ(2πrdr)
Potential due to this element at any point P on the axis of the disc, where OP=z is
dV=q4π∈0z'=σ2πrdr4π∈0√r2+z2
Potential at P due to charge on the entire circular disc
V=πσ4π∈0∫R02rdr√r2+z2=2πσ4π∈0[√r2+z2]R0=2πσ4π∈0[√R2+z2−z]
Using (i), V=2Q4π∈0R2[√R2+z2−z]
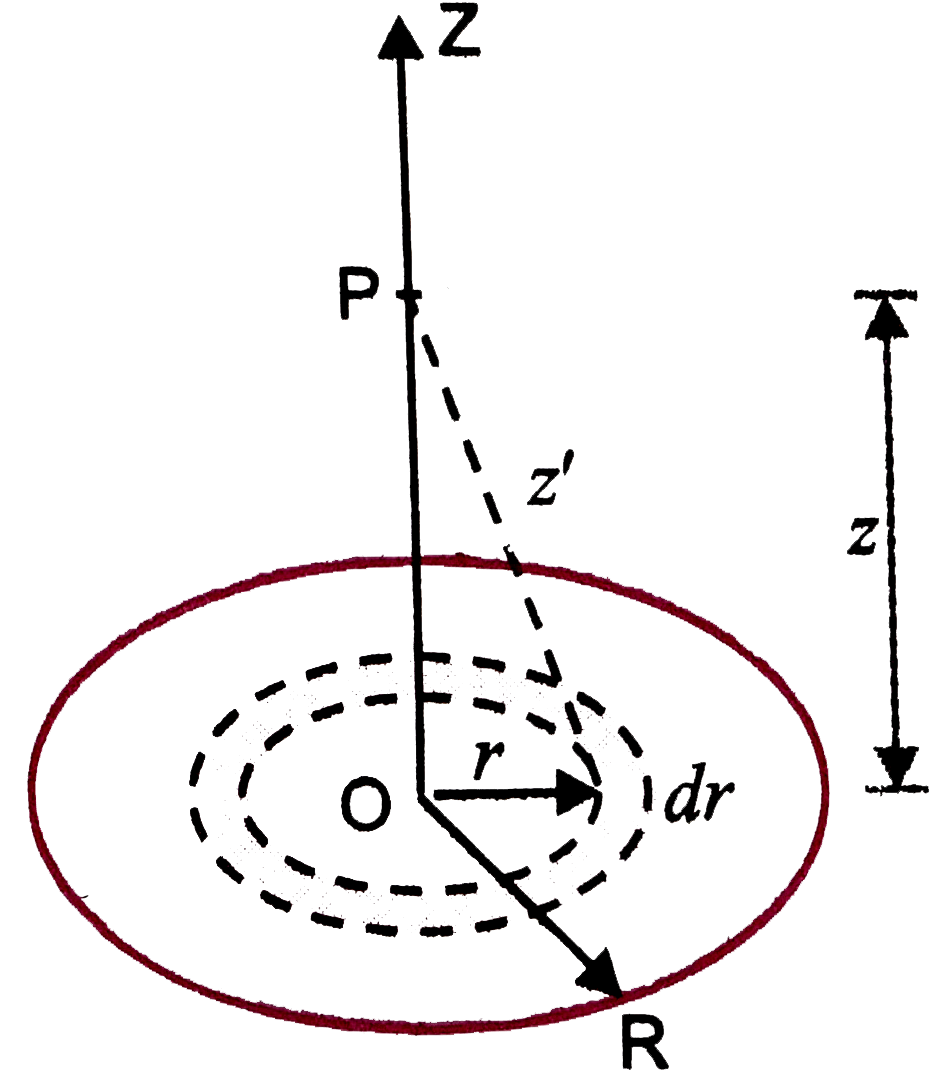
Similar Questions
Knowledge Check
A thin annular disc of outer radius R and R2 inner radius has charge Q uniformly distributed over its surface. The disc rotates about its axis with a constant angular velocity ω. Choose the correct option(s):
AThe magnetic field intensity at the centre of the disc is μ0Qω3πRBThe magnetic field intensity at the centre of the disc is μ0Qω4RCThe magnetic moment of the disc is 5QωR216DThe magnetic moment of the disc is 3QωR24A non conducting disc of radius R, charge q is rotating about an axis passing through its centre and perpendicular to its plane with an angular velocity ω charge q is uniformly distributed over its surface. The magnetic moment of the disc is
A14qωR2B12qωRCqωRD12qωR2
A metallic sphere of radius R has a small bulge of hemispherical shape on its surface. The radius of the bulge is r. If a charge Q is given to the sphere, calculate the quantity of charge on the surface of the bulge. Assume that charge is uniformly distributed on the surface of the bulge (though it is wrong !) and also on the remaining surface of the sphere.
View SolutionCalculate electric field due to a charge uniformly distributed in a spherical volume
View SolutionA point charge Q is placed at the origin . Find the electrostatic energy stored outside the sphere of radius R centred at the origen.
View SolutionA plastic disc of radius 'R' has a charge 'q' uniformly distributed over its surface. If the dis is rotated with a frequency 'f' about its axis, then the magnetic induction at the centre of the disc is given by
View SolutionFind out energy stored inside a solid non-conducting sphere of total charge Q and radius R. [Assume charge is uniformly distributed in its volume.]
View SolutionA non-conducting sphere of radius R is given a charge Q. Charge is uniformly distributed in its volume. The electric potential at centre and at the surface of sphere respectively are
View Solution

