Two capacitors, one of 4μF and the other of 5μF, are connected in parallel and then charged on a 100 V supply. The charge on each capacitor is respectively
0.4 mC and 0.5 mC
0.4 mC and 0.8 mC
4 mC and 5 mC
4 mC and 8 mC
The correct Answer is:A
To solve the problem of finding the charge on each capacitor when they are connected in parallel to a 100 V supply, we can follow these steps:
1. Identify the Values of the Capacitors:
- Capacitor C1=4μF
- Capacitor C2=5μF
2. Understand the Configuration:
- The capacitors are connected in parallel. In a parallel connection, the voltage across each capacitor is the same.
3. Determine the Voltage:
- The supply voltage V=100V.
4. Calculate the Charge on Capacitor C1:
- The formula for charge Q on a capacitor is given by:
Q=C×V
- For C1:
Q1=C1×V=4μF×100V
- Convert μF to Farads:
Q1=4×10−6F×100V=4×10−4C
- Thus, Q1=0.4mC (milliCoulombs).
5. Calculate the Charge on Capacitor C2:
- For C2:
Q2=C2×V=5μF×100V
- Convert μF to Farads:
Q2=5×10−6F×100V=5×10−4C
- Thus, Q2=0.5mC.
6. Final Answers:
- The charge on the 4 µF capacitor Q1=0.4mC.
- The charge on the 5 µF capacitor Q2=0.5mC.
Summary of Charges:
- Charge on C1 (4 µF): 0.4mC
- Charge on C2 (5 µF): 0.5mC
---
- Capacitor C1=4μF
- Capacitor C2=5μF
- The capacitors are connected in parallel. In a parallel connection, the voltage across each capacitor is the same.
- The supply voltage V=100V.
- The formula for charge Q on a capacitor is given by:
Q=C×V
- For C1:
Q1=C1×V=4μF×100V
- Convert μF to Farads:
Q1=4×10−6F×100V=4×10−4C
- Thus, Q1=0.4mC (milliCoulombs).
- For C2:
Q2=C2×V=5μF×100V
- Convert μF to Farads:
Q2=5×10−6F×100V=5×10−4C
- Thus, Q2=0.5mC.
- The charge on the 4 µF capacitor Q1=0.4mC.
- The charge on the 5 µF capacitor Q2=0.5mC.
- Charge on C1 (4 µF): 0.4mC
- Charge on C2 (5 µF): 0.5mC
Topper's Solved these Questions
Similar Questions
Knowledge Check
Two capacitors each of 1μF capacitance are connected in parallel and are then charged by 200 V. The total energy of their charges is
A0.01 JB0.02 JC0.04 JD0.06 JThe charge on capacitor 4μF is
 A2μCB6μCC10μCD12μC
A2μCB6μCC10μCD12μCTwo capacitors of 10μF and 20μF are connected in series with a 30V battery. The charge on the capacitors will be, respectively
A100μC,200μCB200μC,100μCC100μC,100μCD200μC,200μC
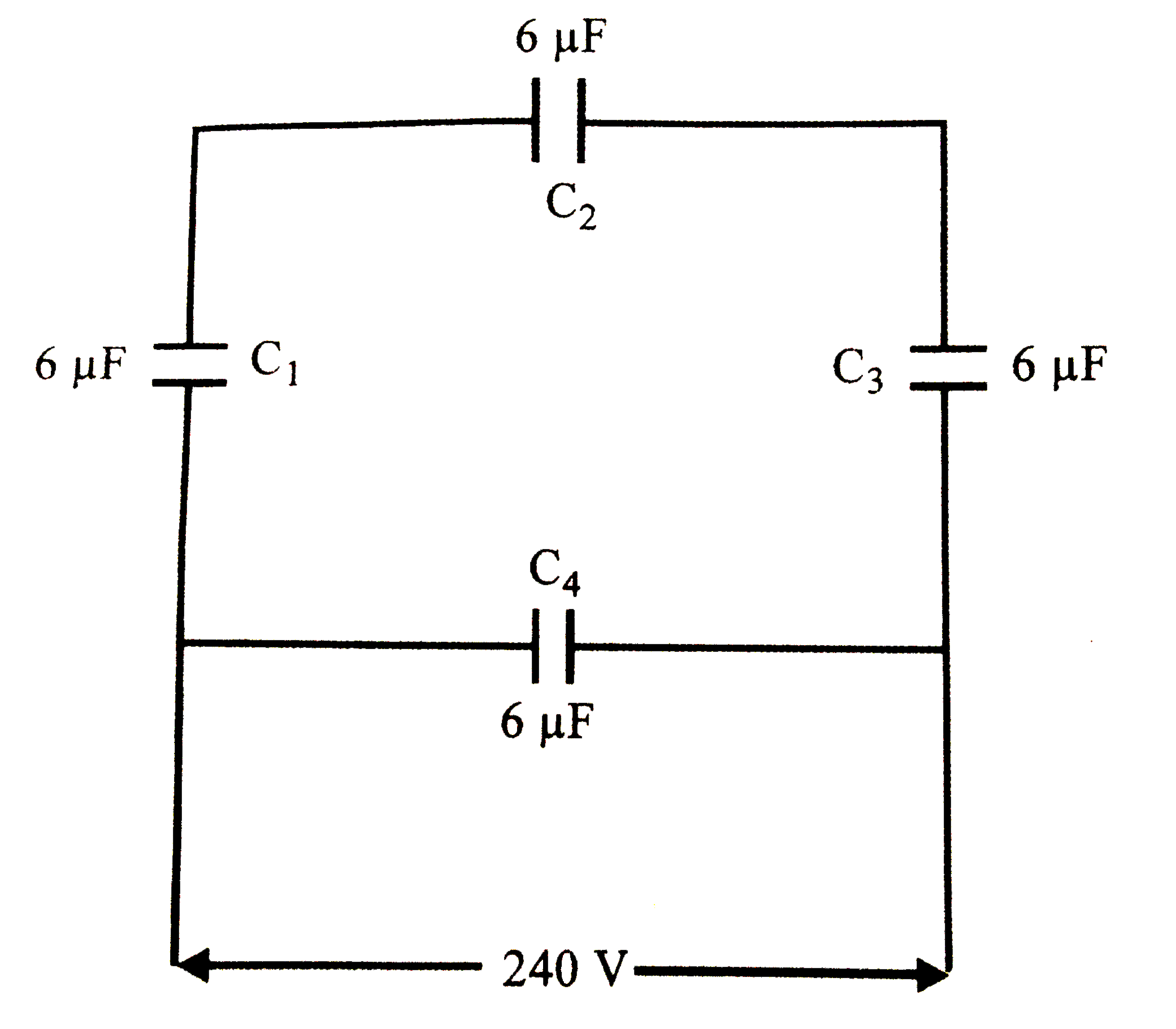
A network of four capacitors of 6 μF each is connected to a 240 V supply. Determine the charge on each capacitor.
View SolutionThe capacitors of 8μF,8μFand4μF are connected in parallel across a source of p.d. 120 V. The total charge on the effective capacity will be
View SolutionTwo capacitors of capacitances 10μFand20μF are connected in series across a potential difference of 100V. The potential difference across each capacitor is respectively
View Solution100 capacitors each having a capacity of 10μF are connected in parallel and are charged by a potential difference of 100kV. The energy stored in the capacitors and the cost of charging them, if electrical energy costs 108 paise per kWh, will be
View SolutionThree capacitors of 3μF,10μFand15μF are connected in series to a voltage supply of 100 V. The charge on 15μF capacitor is
View Solution


