An infinite number of capacitors, having capacitances 1μF,2μF,4μFand8μF….. are connected in series. The equivalent capacitance of the system is
infinite
0.25μF
0.5μF
2μF
The correct Answer is:C
To find the equivalent capacitance of an infinite number of capacitors connected in series with capacitances of 1μF,2μF,4μF,8μF,…, we can follow these steps:
1. Identify the Series Capacitance Formula:
For capacitors in series, the reciprocal of the equivalent capacitance Cs is given by:
1Cs=1C1+1C2+1C3+…
2. List the Capacitors:
The given capacitors are:
C1=1μF,C2=2μF,C3=4μF,C4=8μF,…
This sequence can be expressed as:
Cn=2n−1μFfor n=1,2,3,…
3. Write the Series Capacitance Equation:
Substitute the values into the series capacitance formula:
1Cs=11+12+14+18+…
4. Recognize the Series as a Geometric Series:
The series can be recognized as a geometric series where:
- First term a=1
- Common ratio r=12
5. Sum the Infinite Geometric Series:
The sum S of an infinite geometric series is given by:
S=a1−r
Here, substituting the values:
S=11−12=112=2
6. Calculate the Equivalent Capacitance:
Thus, we have:
1Cs=2⟹Cs=12μF=0.5μF
Final Answer:
The equivalent capacitance of the system is:
Cs=0.5μF
For capacitors in series, the reciprocal of the equivalent capacitance Cs is given by:
1Cs=1C1+1C2+1C3+…
The given capacitors are:
C1=1μF,C2=2μF,C3=4μF,C4=8μF,…
This sequence can be expressed as:
Cn=2n−1μFfor n=1,2,3,…
Substitute the values into the series capacitance formula:
1Cs=11+12+14+18+…
The series can be recognized as a geometric series where:
- First term a=1
- Common ratio r=12
The sum S of an infinite geometric series is given by:
S=a1−r
Here, substituting the values:
S=11−12=112=2
Thus, we have:
1Cs=2⟹Cs=12μF=0.5μF
The equivalent capacitance of the system is:
Cs=0.5μF
Topper's Solved these Questions
Similar Questions
Knowledge Check
An infinite number of identical capacitors each of capacitance 1μF are connected 1μF are connected as shown in Fig. Then the equivalent capacitance between A and B is
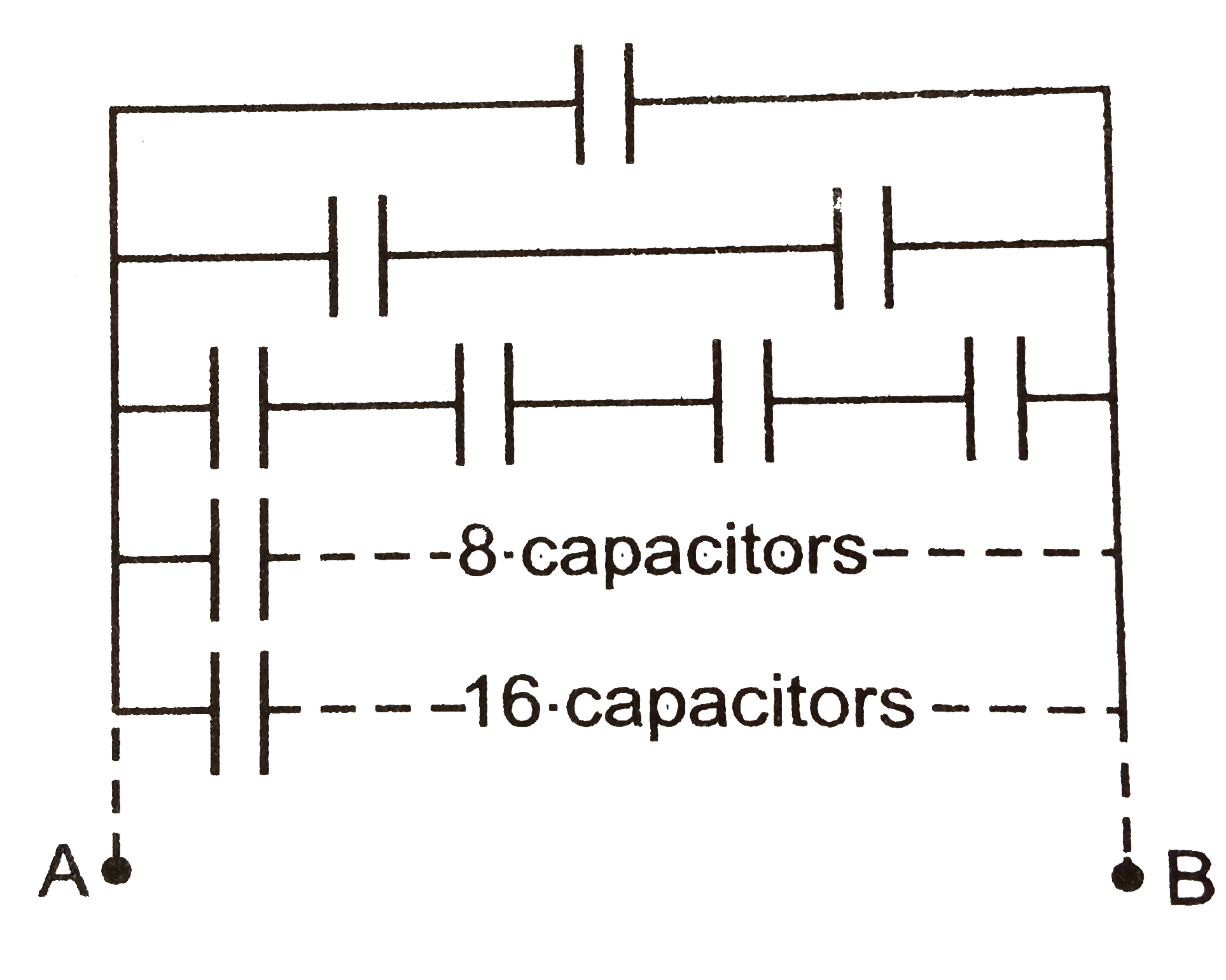 A1μFB2μFC12μFD∞
A1μFB2μFC12μFD∞If two capacitors 2μFand6μF are put in series. The effective capacitance of the system will be
A8μFB4μFC3μFD3/2μFThree capacitors 2μF,3,μFand6μF are joined'in series with each other.
The equivalent capacitance is:A12μFB1μFC2μFD11μF
Three capacitances of capacity ,10 muF, 5 muF" and "5muF" are connected in parallel.The total capacity will be
View SolutionThree capacitors of capacitances 3μF,9μF and 18μF are connected one in series and another time in parallel. The ratio of equivalent capacitance in the two cases (CsCp) will be
View SolutionFour capacitors, each of capacitance 4μF, are connected as shown here. The equivalent capacitance between the points A and B will be
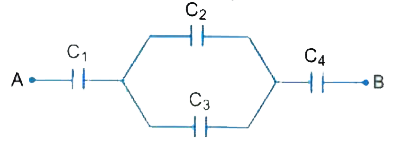
View SolutionThree capacitors each of capacitance 1μF are connected in parallel. To this combination, a fourth capacitor capacitance 1μF is connected in series. The resultant capacitance of the system is
View SolutionThree capacitors X=1μF,Y=2μF and Z=3μF are connected as shown in figure, then the equivalent capacitance between points A and B is
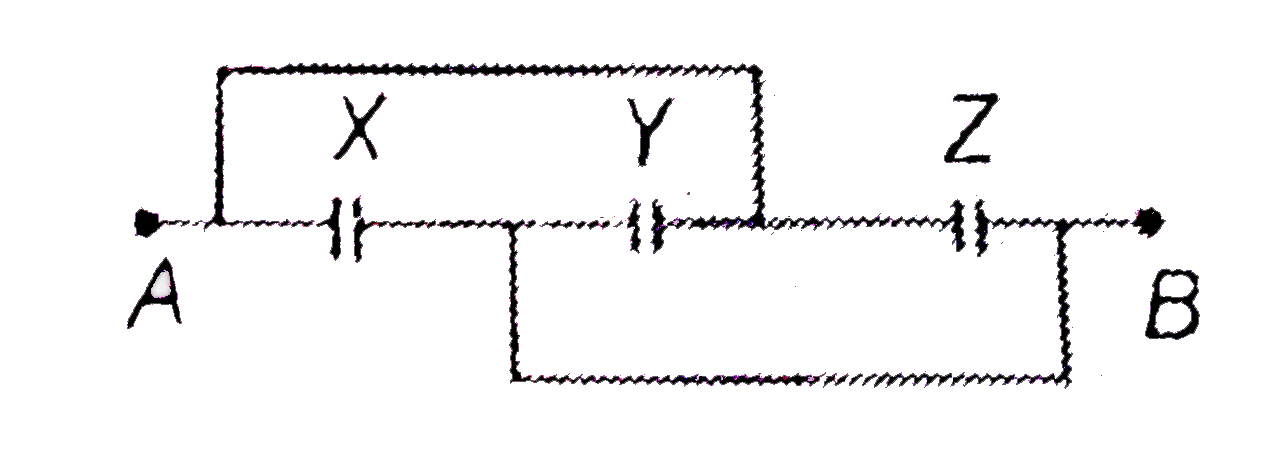
View Solution

