Angular acceleration of a body of mass 50 kg under the action of a torque of magnitude 500 Nm is 25 rad/s2. Then radius of gyration of the body about its axis of rotation is nearly equal to
0.2 m
0.6 m
0.4 m
1 m
The correct Answer is:B
τ=I∝
I=τ∝=50025=20
K=√IM=√2050=√0.4=0.6m.
Topper's Solved these Questions
Similar Questions
Statement-1 : Radius of gyration of a body is a constant quantity.
Statement-2 : The radius of gyration of a body about an axis of rotation may be defined as the root mean square distance of the particles of the body from the axis of rotation.
View SolutionA body of mass 1.5kgrotating about an axis with angular velocity of0.3rads–1 has the angular momentum of 1.8kgm2s–1. The radius of gyration of the body about an axis is
View Solution
Knowledge Check
A torque of magnitude 500 Nm acts on a body of mass 16 kg and produces and angular acceleration of 20 rad/s2. The radius of gyration of the body is
A54mB45mC23mD32mA toraue of magnitude 4000 N-m, acts on a body of mass 2 kg. If the angular acceleration produced in the body is 20 rad/s2, then the radius of gyration of the body is
A5 mB10 mC15 mD20 mIf the kinetic energy of rotation of a body about an axis is 9 J and the moment of inertia is 2 kg m2, then the angular velocity of the body about the axis of rotation in rad/s is
A2B3C1D9
A flywheel rotating about a fixed axis has a kinetic energy of 225 J when its angular speed is 25 rad/s. The angular momentum of the flywheel about its axis of rotation is
View SolutionThe rotational kinetic energy of a body is E. In the absence of external torque, the mass of the body is halved and its radius of gyration is doubled. Its rotational kinetic energy is
View SolutionA toruque τ produces an angular acceleration in a body rotating about an axis of rotation. The moment of inertia of the body is increased by 50% by redistributing the masses, about the axis of rotation. To maintain the same angular acceleration, the torque is changed to τ'. What is the relation between τandτ'?
View SolutionWhen a body is hinged at a point and a force is acting on the body in such a way that the line of action of force is at some distance from the hinged point, the body will start rotating about the hinged point. The angular acceleration of the body can be calculated by finding the torque of that force about the hinged point. A disc of mass m and radius R is hinged at point A at its bottom and is free to rotate in the vertical plane. A force of magnitude F is acting on the ring at top most point.
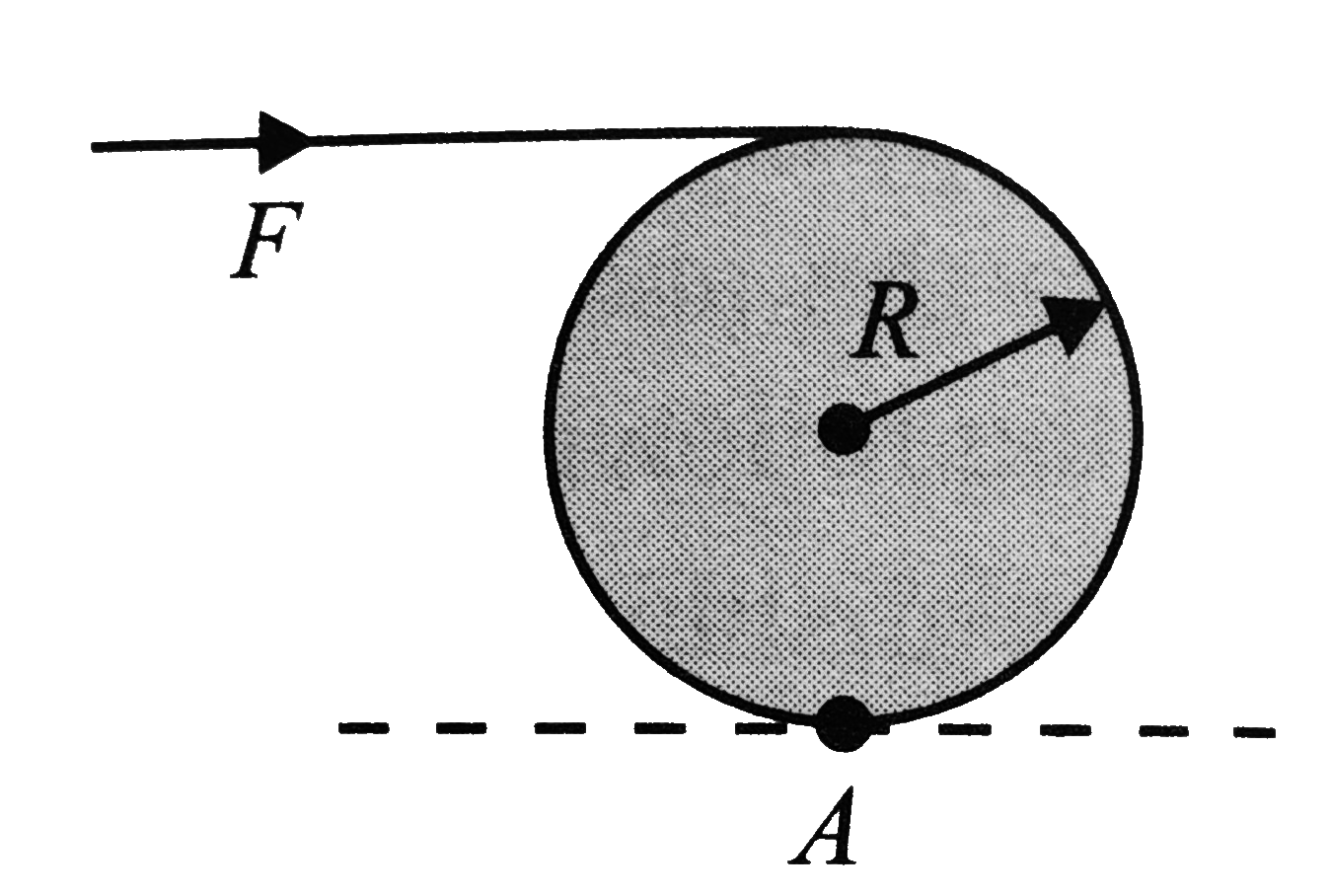
Tangential acceleration of the centre of mass is
View SolutionThe radius of gyration of a body about an axis at a distance of 4cm from its centre of mass is 5cm. The radius of gyration about a parallel axis through centre of mass is
View Solution

