A toruque τ produces an angular acceleration in a body rotating about an axis of rotation. The moment of inertia of the body is increased by 50% by redistributing the masses, about the axis of rotation. To maintain the same angular acceleration, the torque is changed to τ'. What is the relation between τandτ'?
A
τ'=τ
B
τ'=23τ
C
τ'=32τ
D
τ'=τ2
Video Solution
Text Solution
The correct Answer is:C
Initially τ=Iα …(1)
In the second case I is increased by 50%.
i.e. I'=(I+50100I)=32I
∴ τ'=I'α=32Iα=32τ
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
A torque of magnitude 2000 Nm acting on a body produces an angular acceleration of 20 rad/s2, The moment of inertia of the body is
A150kgm2B50kgm2C200kgm2D100kgm2For a rotating body about fixed axis ,
Aevery particle moves in a circleBthe linearvelocity is related to angular velocityCBoth (1) and (2) are correctDBoth (1) and (2) are incorrectA rod AB of mass m and length l is rotating about a vertical axis as shown. It's moment of inertia about this axis is :
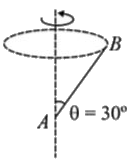 Aml23Bml24Cml216Dml212
Aml23Bml24Cml216Dml212
Obtain an expressing for torque acting on a body rotating with uniform angular acceleration.
View SolutionIf the angular velocity of a rotating rigid body is increased then its moment of inertia about that axis
View SolutionThe moment of inertia of a body about a given axis of rotation depends upon :-
View SolutionA fly wheel rotating about a fixed axis has a kinetic energy of 360J. When its angular speed is 30rads−1. The moment of inertia of the wheel about the axis of rotation is
View SolutionIf the kinetic energy of rotation of a body about an axis is 9 J and the moment of inertia is 2 kg m2, then the angular velocity of the body about the axis of rotation in rad/s is
View Solution

