A ring and a thin hollow cylinder have the same mass and radius. If Ir and Is represent their moment of inertia about their axes, then
Ir=2Is
Is=2Ir
Is=Ir
none of these
The correct Answer is:C
As mass and radius of ring = mass and radius of hollow cylinder.
Topper's Solved these Questions
Similar Questions
One circular ring and one circular disc, both are having the same mass and radius. The ratio of their moments of inertia about the axes passing through their centres and perpendicular to their planes, will be
View SolutionA semi-circular ring has mass m and radius R as shown in figure. Let I1,I2,I3 and I4 be the moments of inertia about the four axes as shown . Axis 1 passes through centre and is perpendicular to plane of ring. Then , match the following.
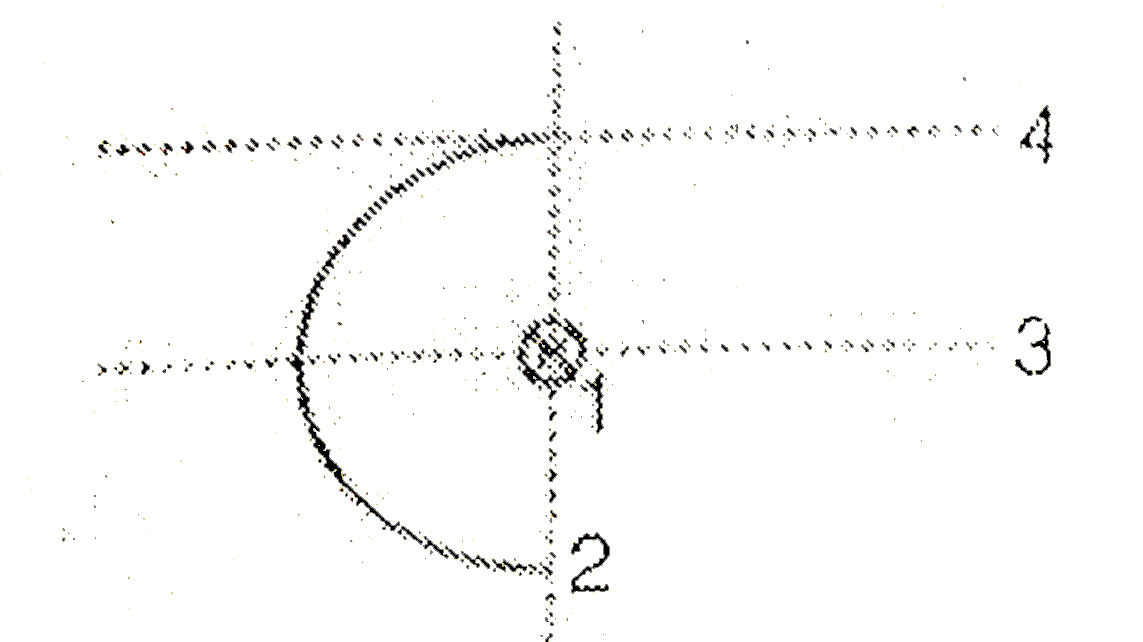

View Solution
Knowledge Check
Two solid spheres of the same mass are of steel and aluminium. If ISandIA denote their moments of inertia about their diameters, then
AIS=IABIS>IACIS<IADnone of the aboveA ring and a disc have same mass and same radius. Then ratio of moment of inertia of ring to the moment of inertia of disc is
A4B2C0.5D1One solid sphere A and another hollow sphere B are of same mass and same outer radii. Their moment of inertia about their diameters are respectively IA and IB such that.
AIA=IBBIA>IBCIA<IBDIA/IB=dA/dB
Four rings each of mass M and radius R are arranged as shown in the figure. The moment of inertia of the system about YY' will be

View SolutionOne solid sphere A and another hollow sphere B are of same mass and same outer radii. Their moments of inertia about their diameters are respectively IA and IB such that
where dA and dB are their densities .
View SolutionA steel ring and a wooden ring have the same mass. Then which will have smaller moment of inertia about the diameter ?
View SolutionA ring and a disc have same mass and same radius. Ratio of moments of inertia of the ring about a tangent in its plane to that of the disc about its diameter is
View SolutionThree rings each of mass M and radius R are arranged as shown in the figure. The moment of inertia of the system about YY¢ will be
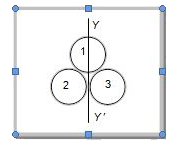
View Solution

