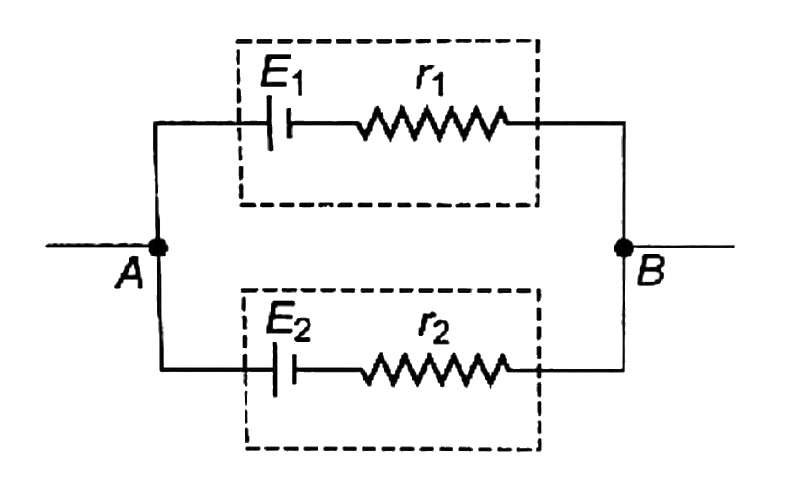
When two cells of emf E1E2 and interval resistance r1 and r2 are connected in parallel between two points A and B, find the values of effective internal resistance of two cells and their effective emf.
To find the effective internal resistance and effective EMF of two cells connected in parallel, we can follow these steps:
Step 1: Understand the Configuration
When two cells with EMFs E1 and E2 and internal resistances r1 and r2 are connected in parallel, they share the same voltage across their terminals.
Step 2: Write the Terminal Voltage Equations
The terminal potential difference (voltage) across each cell can be expressed as:
- For cell 1:
V=E1−I1r1
- For cell 2:
V=E2−I2r2
Step 3: Apply Kirchhoff's Current Law
According to Kirchhoff's Current Law, the total current I flowing out of the junction is the sum of the currents through each cell:
I=I1+I2
Step 4: Express Currents in Terms of Voltage
From the terminal voltage equations, we can express I1 and I2:
- Rearranging the first equation gives:
I1=E1−Vr1
- Rearranging the second equation gives:
I2=E2−Vr2
Step 5: Substitute Currents into the Total Current Equation
Substituting I1 and I2 into the total current equation:
I=E1−Vr1+E2−Vr2
Step 6: Solve for Voltage V
Rearranging gives:
I=E1r1+E2r2−V(1r1+1r2)
This can be rearranged to find V:
V(1r1+1r2)=E1r1+E2r2−I
Thus,
V=E1r1+E2r2−I1r1+1r2
Step 7: Find Effective EMF
The effective EMF Eeff is given by:
Eeff=E1r2+E2r1r1+r2
Step 8: Find Effective Internal Resistance
The effective internal resistance reff is given by:
reff=r1r2r1+r2
Final Result
Thus, the effective EMF and effective internal resistance of the two cells connected in parallel are:
- Effective EMF:
Eeff=E1r2+E2r1r1+r2
- Effective Internal Resistance:
reff=r1r2r1+r2
When two cells with EMFs E1 and E2 and internal resistances r1 and r2 are connected in parallel, they share the same voltage across their terminals.
The terminal potential difference (voltage) across each cell can be expressed as:
- For cell 1:
V=E1−I1r1
- For cell 2:
V=E2−I2r2
According to Kirchhoff's Current Law, the total current I flowing out of the junction is the sum of the currents through each cell:
I=I1+I2
From the terminal voltage equations, we can express I1 and I2:
- Rearranging the first equation gives:
I1=E1−Vr1
- Rearranging the second equation gives:
I2=E2−Vr2
Substituting I1 and I2 into the total current equation:
I=E1−Vr1+E2−Vr2
Rearranging gives:
I=E1r1+E2r2−V(1r1+1r2)
This can be rearranged to find V:
V(1r1+1r2)=E1r1+E2r2−I
Thus,
V=E1r1+E2r2−I1r1+1r2
The effective EMF Eeff is given by:
Eeff=E1r2+E2r1r1+r2
The effective internal resistance reff is given by:
reff=r1r2r1+r2
Thus, the effective EMF and effective internal resistance of the two cells connected in parallel are:
- Effective EMF:
Eeff=E1r2+E2r1r1+r2
- Effective Internal Resistance:
reff=r1r2r1+r2
Topper's Solved these Questions
- COMMUNICATION SYSTEMSBook:PRADEEPChapter:COMMUNICATION SYSTEMSExercise:MODEL TEST PAPER-2
Explore 9 Videos
- COMMUNICATION SYSTEMSBook:PRADEEPChapter:COMMUNICATION SYSTEMSExercise:Multiple Choice Question
Explore 4 Videos
- ATOMS AND NUCLEIBook:PRADEEPChapter:ATOMS AND NUCLEIExercise:Assertion- Reason type question 12
Explore 1 Video
- CURRENT ELECTRICITYBook:PRADEEPChapter:CURRENT ELECTRICITYExercise:Problems for Practice (B)
Explore 2 Videos
Similar Questions
Knowledge Check
Two batteris of emf ε1 and ε2 wit respective internal resistance r1 and r2 are connected in parallel. Now
AThe effective emf of this parallel combination is (ε1r1+ε2r2)(r1+r2)BThe effective internal resistance of this combination is 2r1r2(r1+r2)Cthe effective emf of this parallel combination is (ε1r2+ε2r1)(r1+r2)DThe effective internal resistance of this combination is r1r2(r1+r2)Two cells of emf 1.25V,0.75V and each of internal resistance 1Ω are connected in parallel. The effective emf will be
A1 VB1.25 VC2 VD0.5 VIf n cells each of emf E and internal resistance are connected in parallel, then the total emf and internal resistances will be
Aε,rnBε,nrCnε,rnDnε,nr
Two cells of emf 2ε and ε and internal resistance 2r and r respectively, are connected in parallel. Obtain the expressions for the equivalent emf and the internal resistance of the combination.
View SolutionTwo cells of emfs ε1andε2 and internal resistances r1andr2 respectively are connected in parallel . Obtain expressions for the equivalent (i) resistance and , (ii) emf of the combination.
View SolutionTwo cells of emf ε1 and ε2 having internal resistances r1 and r2 respectively are connected in parallel as shown in Fig. Deduce the expressions for the equivalent emf and equivalent internal resistance of a cell which can replace the combination between the pointsB1 and B2 .

View SolutionTwo cells of equal e.m.f. E b ut of difference internal resistance r1 and r2 are connected in parallel and the combination is connected with an external resistance R to obtain maximum power in R. find the value of R

View SolutionTwo batteries of emf E1 and E2(E2>E1) and internal resistance r1 and r2 respectively are connected in parallel as shown in the figure. Then, which of the followings statements is correct ?
View Solution

