Question

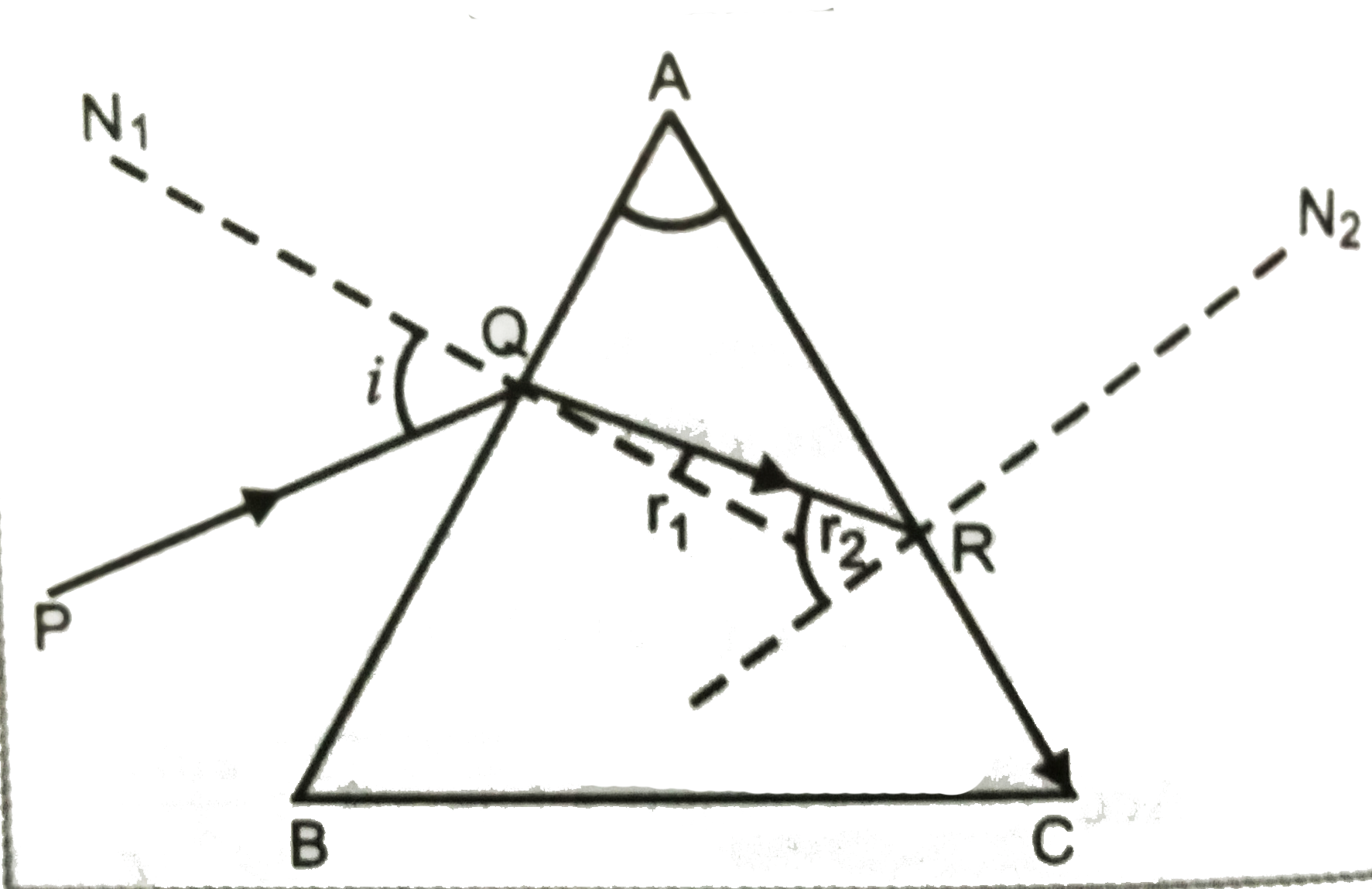
The refracting angle of a glass prism is ${\displaystyle {60}^{\circ }}$ and ${\displaystyle \mu }$ of its material is ${\displaystyle 1.45}$. Calculate angle of incidence at the first that will just reflect internaly the ray at the second face.

Answer

`24.2^(@)`

Explanation

Here, `A = 60^(@), mu = 1.45, i_(1) = ?`
From `mu = (1)/(sin C)`,
`sin C = (1)/(mu) = (1)/(1.45) = 0.6897`
`C = sin^(-1) (0.6897) = 43.6^(@)`
For total internal relfection at 2nd face of prism,
`r_(2) = C = 43.6^(@)`
From `r_(1) + r_(2) = A`,
`r_(1) = A - r_(2) = 60^(@) - 43.6^(@) = 16.4^(@)`
From `mu = (sin i_(1))/(sin r_(1))`,
`sin i_(1) = mu sin r_(1) = 1.45 xx sin 16.4^(@)`
`= 1.45 xx 0.2823 = 0.4093`
`:. i_(1) = sin^(-1) (0.4093) = 23.2^(@)`