A light rays is incident on a prism of prism angle A and refractive index μ. Show that the smallest value of the angle of incidence for which the reflected ray does not suffer total internal reflection at the second face, i.e. just comes out of it, is given by
i=sin−1[(μ2−1)1/2sinA−cosA].
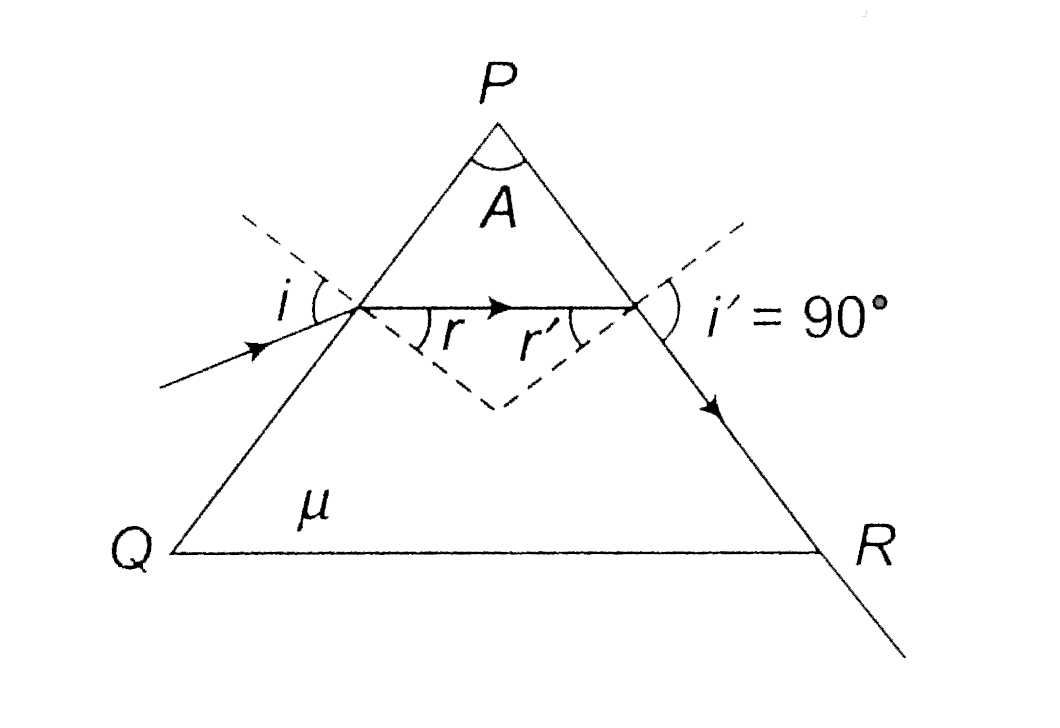
i′=90∘ i.e. r′=C, sinC=1/μ
r+r′=A
r+C=A⇒r=A−C
Refraction on PQ:
1×sini=μsinr=μsin(A−C)
=μ(sinAcosC−cosAsinC)
=μ[sinA√1−sin2C−cosAsinC]
=μ[sinA√1−1μ2−cosA⋅1μ]
=μ[sinA√μ2−1−cosAμ]
=sinA√μ2−1−cosA
i=sin−1[sinA√μ2−1−cosA]
Topper's Solved these Questions
- REFRACTION OF LIGHT BY PLANE SURFACESBOOK - CP SINGHCHAPTER - REFRACTION OF LIGHT BY PLANE SURFACESEXERCISE - Exercises
110 Videos
- REFRACTION AT SPHERICAL SURFACESBOOK - CP SINGHCHAPTER - REFRACTION AT SPHERICAL SURFACESEXERCISE - EXERCISES
105 Videos
- SEMICONDUCTORSBOOK - CP SINGHCHAPTER - SEMICONDUCTORSEXERCISE - Exercises
140 Videos
Similar Questions
A ray of light falls on a glass plate of refractive index μ=1.5.
What is the angle of incidence of the ray if the angle between the reflected and
refracted rays is 90∘?
View SolutionThe refractive index of the core of an optical fibre is μ2 and that of the cladding is μ1 .The angle of incidence on the face of the core so that the light ray just under goes total internal reflection at the cladding is
View Solution
Knowledge Check
Light ray is incident on a prism of angle A=60∘and refractive indexμ=√2.the angle of incidence at which the emergent ray grazes the surface is given by
Asin−1(√3−12)Bsin−1(1−√32)Csin−1(√32)Dsin−1(2√3)Light ray is incident on a prism of angle A=60∘ are refractive index μ=√2. The angle of incidence which the emergent rays grazes the surface is given
Asin−1(√3−12)Bsin−1(√2−12)Csin−1(√32)Dsin−1(23√3)The angle of incidence at which reflected light is totally polarized for reflection form air to glass ( refraction index μ) is
Asin−1(μ)Bsin−1(1μ)Ctan−1(1μ)Dtan−1(μ)
The refractive index of the material of a prism of refracting angle 74∘ is 1.66 for a certain monochromatic ray. What should be the minimumangle of incidence of this ray on the prism so that no total internal reflection takes place as they come out of the prism.
View SolutionA ray of light suffers minimum deviation when incident on an equilateral prism of refractive index √2 . What is the angle of incidence ?
View SolutionA ray of light incident on a prism of angle 60∘, does not emerge out. Refractive index of material of prism may be
View SolutionLight ray is travelling from a medium of refractive index μ in to air. Angle of incidence at the interface is 53∘. Light ray is found to suffer total internal reflection. Select possible values of μ from the following :
View SolutionA ray of light suffers a minimum deviation when incident on an equilateral prism of refractive index √2 The angle of incidence is
View Solution
