A ray of light enters the face AB of a glass prism of refractive index μ at an angle of incidence i. Find the value of i such that no ray emerges from the face AC of the prism, given angle of prism is A.
As shown in Fig. no ray will emerge from face AC of the prism, when light undergoes total internal reflection at R for which, r2=C, the critical angle.
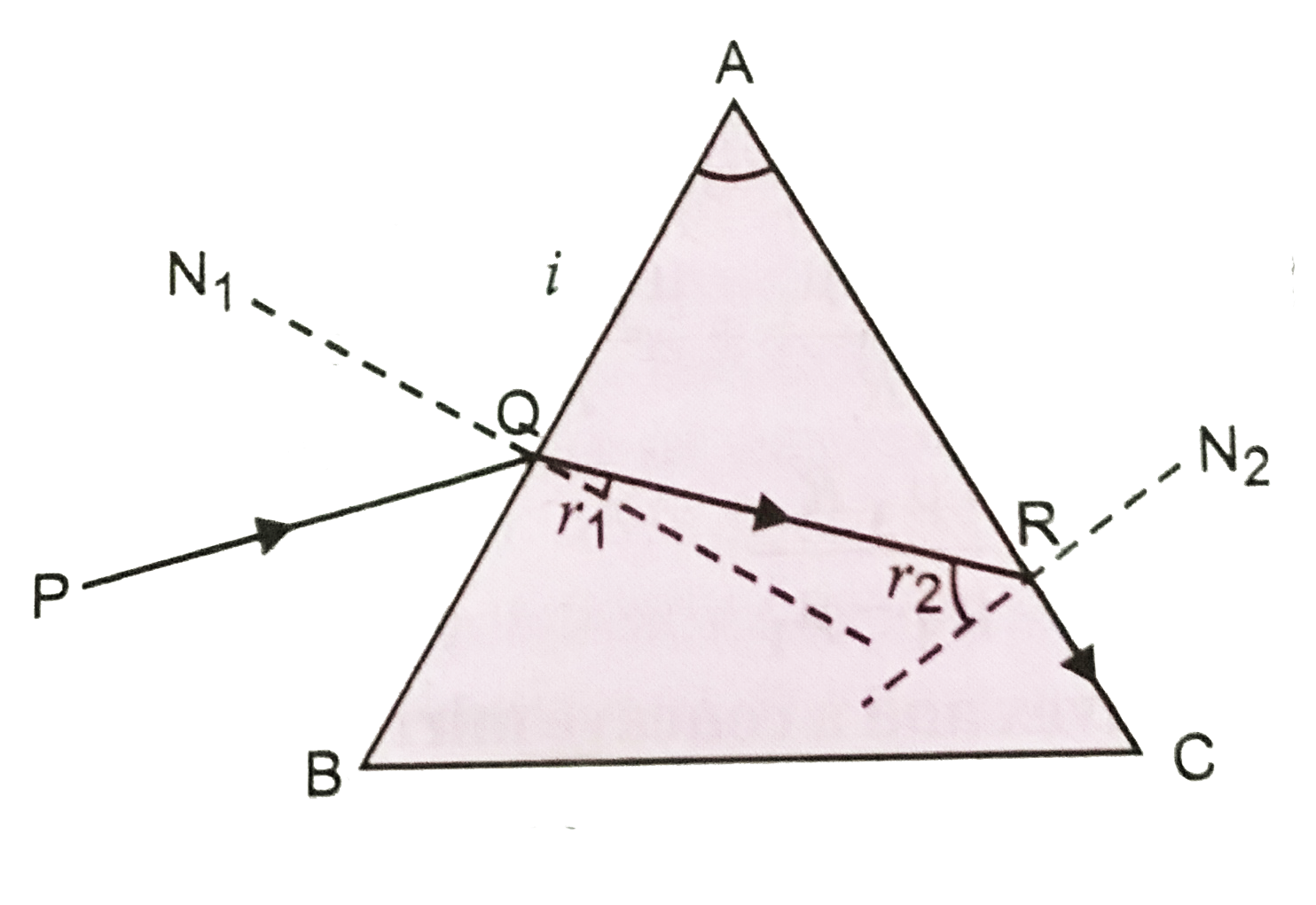 ltbr> As sinC=1μ=sin2
ltbr> As sinC=1μ=sin2
∴μsinr2=1 ...(i)
As r1+r2=A,r1=A−r2
From Snell's Law,
sini=μsinr1=μsin(A−r2)
=μ(sinAcosr2−cosAsinr2)
sini=μsinAcosr2−μsinr2cosA
using (i), sini=μsinAcosr2−cosA ... (iii)
From (i), sinr2=1μ
∴cosr2=√1−sin2r2=√1−1μ2
Put in (iii),
sini=μsinA√1−1μ2−cosA
Hence, i=sin−1[μsinA√1−1μ2−cosA]
Topper's Solved these Questions
- OPTICSBook:PRADEEPChapter:OPTICSExercise:Very short answer question
Explore 5 Videos
- OPTICSBook:PRADEEPChapter:OPTICSExercise:very short answer questions
Explore 1 Video
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:PRADEEPChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Competition Focus (Multiple Choice Questions)
Explore 2 Videos
Similar Questions
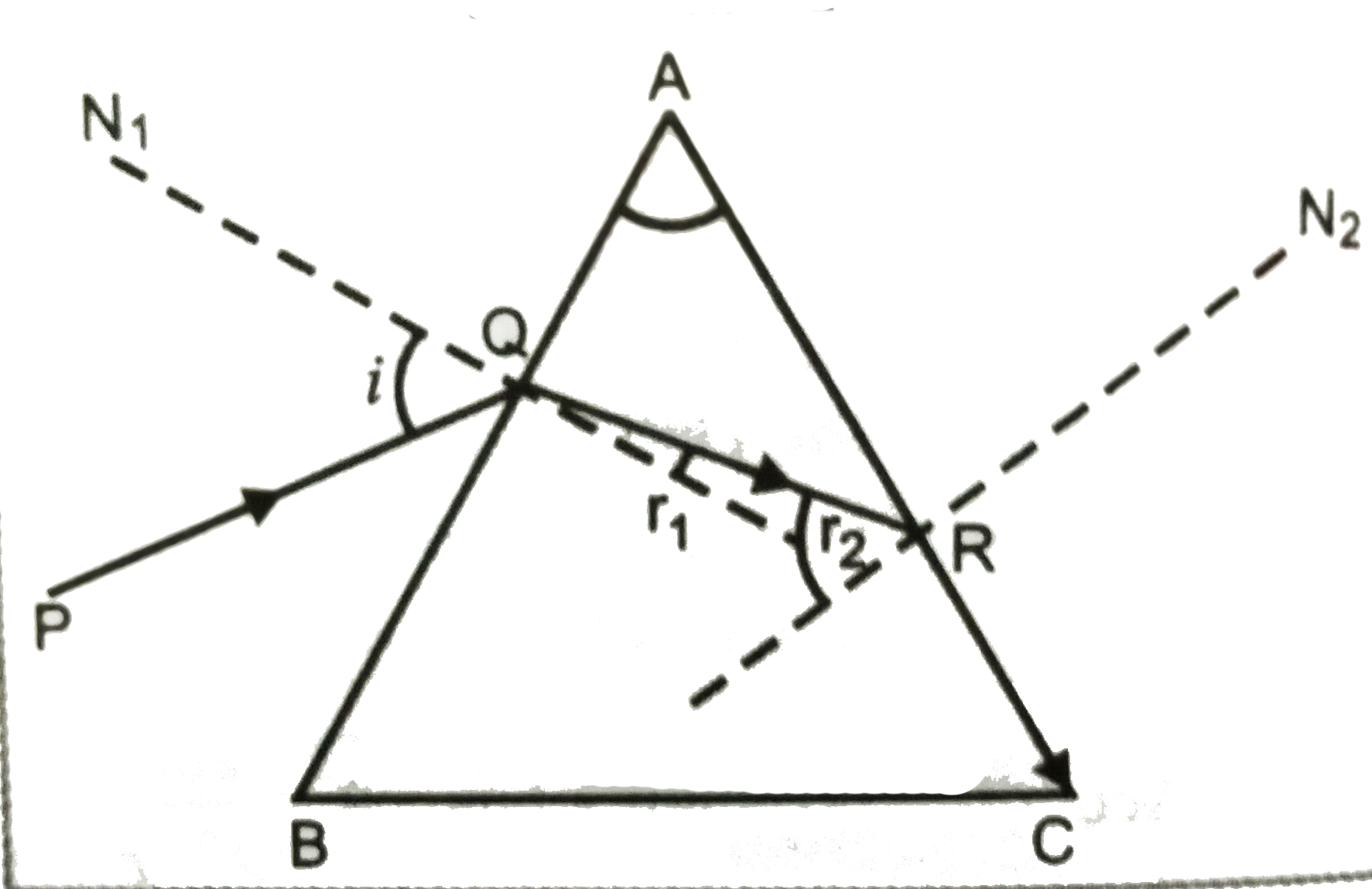
A ray of light the face AB of a glass prism of refractive index μ at an angle of incidence i. Find the value of i such that no ray emerges from the face AC of the prism. Given angle of prism is A.
View SolutionA ray of light incident normally on the first face of a glass prism of refractive index 1.6 just emerges from the other face. Find the angle of the prism.
View Solution
Knowledge Check
Light falls at normal incidence on one face of a glass prism of refractive index √2. Then the angle of emergence when the angle of the prism is 45∘
A45°B60°C15°D90°A glass prism has a refractive angle of 90∘ and a refractive index of 1.5. A ray is incident at an angle of 30∘. The ray emerges from an adjacent face at an angle of
A60∘B30∘C45∘Dthe ray does not emergeA ray of light is incident normally on one of the equal faces of a right isosceles prism of refractive index 1.5. The angle between incident and emergent rays is
A45∘B90∘C180∘D0∘
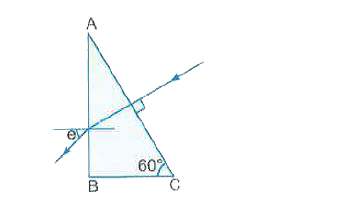
Calculate the angle of emergence (e) of the ray of light incident normally on the face AC of a glass prism ABC of refractive index √3. How will the angle of emergence change qualitatively, if the ray of light emerges from the prism into a liquid of refractive index 1.3 instead of air ?
View SolutionA ray of light falls on a glass prism at a angle of incidence of 30∘. Find the direction of the emergent ray if the angle of the prism is 60∘ and refractive index is 1.50
View SolutionA ray of light is incident on a glass prism of refractive index μ and refractive angle A. If it just suffers total internal reflection at the other face, obtain an expression relating the angle of incidence , angle of prism and critical angle.
View SolutionA ray of light takes grazing incidence on the first face of a prism having critical angle C. Find the angle of prism is after refraction ray does not emerge out.
View SolutionLight ray is incident on a prism of angle A=60∘ are refractive index μ=√2. The angle of incidence which the emergent rays grazes the surface is given
View Solution

