An equilateral glass prism is immersed in water . Calculate the angle of deviation produced for a ray of light incident at on one face of the prism.
For an equilateral glass prism,
and

For refraction on face , Fig.
As
Again
Angle of deviation,
Topper's Solved these Questions
- OPTICSBook:PRADEEPChapter:OPTICSExercise:Very short answer question
Explore 5 Videos
- OPTICSBook:PRADEEPChapter:OPTICSExercise:very short answer questions
Explore 1 Video
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:PRADEEPChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Competition Focus (Multiple Choice Questions)
Explore 2 Videos
Similar Questions
An equilateral glass prism of refractive index 1.5 is immersed in water. Find the angle of deviation produced when a ray of light is incident at 42∘ on one face of the prism.
(Refractive index of water = 1.33)
View SolutionA glass prism of angle 72∘ and refractive index 1.66 is immersed in a liquid of μ=1.33. Calculate the angle of minimum deviation.
View Solution
Knowledge Check
A thin glass prism of μ=1.5 is immersed in water of μ=1.33 . The ratio of deviation of the ray in water to that in air for the same prism is
A1:4B1:2C1:8D1:3An equilateral prism produces an angle of deviation 60∘ when the angle of incidence is 60∘. The angle of deviation produced when the ray is incident normal to the surface is
A30∘B45∘C60∘Dcan't be determined
Light is incident from glass (μ=1.50) to water (μ=1.33) find the range of the angle of deviation for which there are two angles of incidence.
View Solution(i) A ray of light incident on face AB of an equilateral glass prism, shows minimum deviation of 30∘. Calculate the speed of the light through the prism.
(ii) Find the angle of incidence at face AB so that the emergent ray grazes along the face AC.
View SolutionFor a glass prism (μ=√3) the angle of minimum deviation is equal to the angle of the prism. Find the angle of the prism.
View SolutionA ray of light passes from glass (μg=1.52) to water (μw=1.33). What is the critical angle of incidence?
View SolutionA ray of light PQ is incident on the face AB of an equilateral glass prism ABC as shown in the figure. Show that angle of emergence = angle of deviation. Also, with a ray diagram, trace the path of the emergent ray.
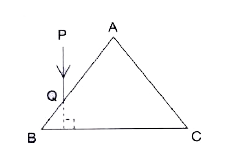
View SolutionA prism is made of glass of unknown refractive index. A parallel beam of light is incident on a face of the prism. By rotating the prism, the minimum angle of deviation is measured to be 40∘. What is the refractive index of the prism ? If the prism is placed in water (μ=1.33), predict the new angle of minimum deviation of the parallel beam. The refracting angle of prism is 60∘.
View Solution
