(i) A ray of light incident on face AB of an equilateral glass prism, shows minimum deviation of 30∘. Calculate the speed of the light through the prism.
(ii) Find the angle of incidence at face AB so that the emergent ray grazes along the face AC.
(i) For minimum deviation,
As prism is equilatral , A=60∘
σ=A2=60∘2=30∘
also, δmin=(μ−1)60∘=30∘
⇒μ=12+1=32
By Snell's Law,
sinisinr=μ1=v1v2
μ=c√2⇒V1=cμ
V1=3×1083/2
V1=2×108ms−1.
(ii) From Snell's law sinisinr=μ21
Here, Angle of Ref. 90∘
So, (sini)λcsin90∘=1√2
or, i=45∘
∠ of refraction at AB is 15∘
So, from Snell's law,
sinAB=sinrAB×μ12=sin−1(√2sin15∘).
Topper's Solved these Questions
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - SET-I (SECTION-D)
1 Video
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - SET-I (SECTION-E)
6 Videos
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - SET-I (SECTION-B)
5 Videos
- SAMPLE PAPER 2019BOOK - XII BOARDS PREVIOUS YEARCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D
6 Videos
Similar Questions
Knowledge Check
A ray of light is incident at an angle of incidence 45∘ on an equilateral prism and emerge at an angle 45∘ then the refractive index of the medium of the prism is:
A2B√2C1√2D√3
A ray of light incident on face AB of an equilateral glass prism, shows minimum deviation of 306∘ .Calculate the speed of light through the prism.
View SolutionIn the above example, find the angle of incidence at face AB, so that emergent ray grazes along the face AC'.
View SolutionA ray of incident on an equilateral prism shows minimum deviation of 30∘ .The speed of light through the prism is ?
View SolutionA ray of light incident at an angle 90° with the face of an equilateral prism passes symmetrically. Calculate the refractive index of the material of the prism
View SolutionA ray of light falls on one face of an equilateral prism at an angle of 40∘ and emerges out at an angole of 37∘ What is the angle of deviation through the prism ?
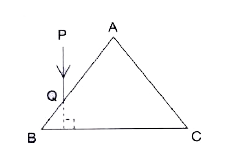
View SolutionA ray of light PQ is incident on the face AB of an equilateral glass prism ABC as shown in the figure. Show that angle of emergence = angle of deviation. Also, with a ray diagram, trace the path of the emergent ray.
View SolutionA ray of light is incident at an angle of 60∘ on the face of a prism having refracting angle 30∘. The ray emerging out of the prism makes an angle 30∘ with the incident ray. Show that the emergent ray is perpendicular to the face through which it emerges.
View Solution