Three studends X,Y and Z performed an experiment for studying variation of a.c. with angular frequency in series LCR circuit, and obtained the graphs shown in Fig. They all used a.c. soucre of same rms value and inductance of same value. What can we conclude about (i) Capacitance value (ii) Resistance value used by them? In which case will the quality factor be maximum? What we conclude about nature of impedance of set up at frequency $ω_{0}$ ?

Video Solution

Text Solution

Verified by Experts

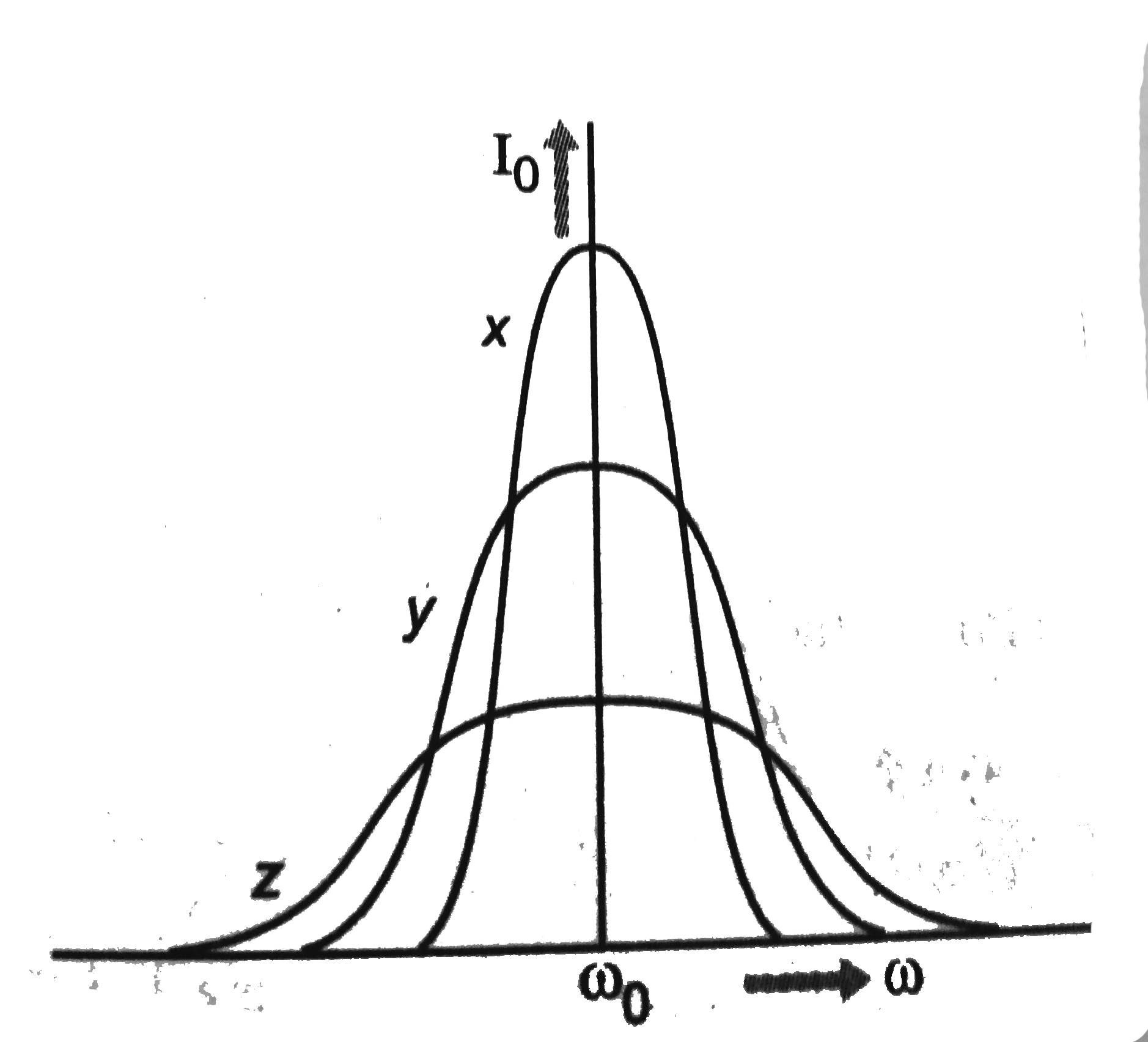
For resonance, $X_{L} = X_{C}$ . As L is same, therefore, capactance used by all the three students must be the same for same value of $ω_{0}$ .
Maximum value of current is inversely proportional to R. Therefore, resistance used by students X is lowest and resistance used by student Z is the highest.
At $ω_{0}$ , impedance is equal to ohmic resistance only.

Updated on:21/07/2023

What can be concluded about the values of $Δ H$ and $Δ S$ from this graph ?

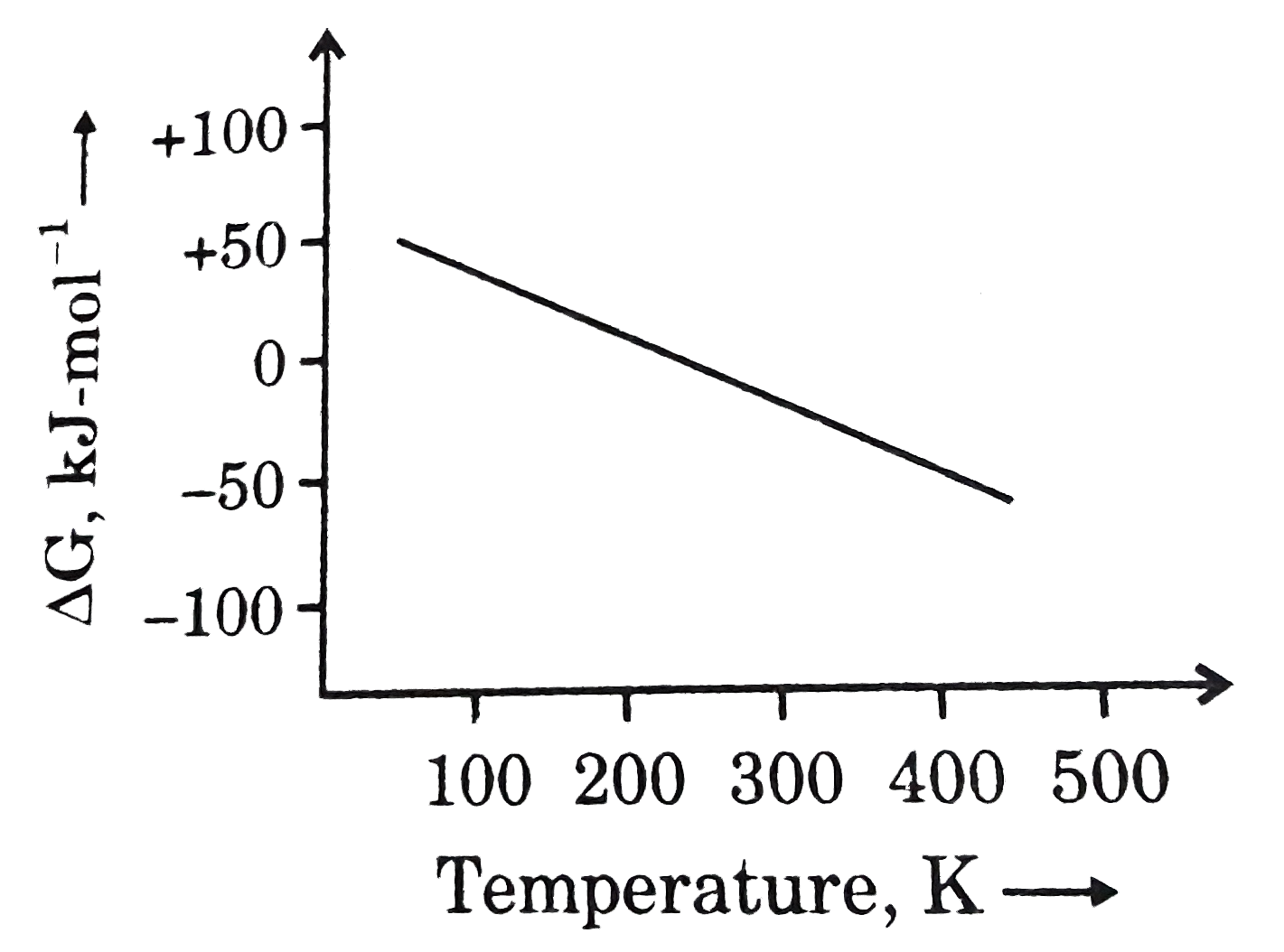A $Δ H > 0, Δ S > 0$
B $Δ H > 0, Δ S < 0$
C $Δ H < 0, Δ S > 0$
D $Δ H < 0, Δ S < 0$
From the matrix equation AB=AC, we conclude B=C provided.
AA is singular
BA is non-singular
CA is symmetric
DA is a square
In an ac circuit shown in fig , the supply voltage has a constant rms value v but variable frequency f. At resonance, the circuit

Ahas current I given by $I = \frac{V}{R}$
Bhas a resonance frequenv=cy 500 Hz
Chas a voltage across the capacitor which is $180^{\circ}$ out of phase with that across the inductor
DHas a current given by $I = \frac{V}{\sqrt{R^{2} + {(\frac{1}{π} + \frac{1}{π})}^{2}}}$