A resistance R and an inductance L are connected in series in an a.c. circut. If $ω$ is the angular frequency of the source, then the power factor is given by

A

$\frac{ω L}{R}$

B

$\frac{R}{ω L}$

C

$\frac{R}{\sqrt{R^{2} + ω^{2} L^{2}}}$

D

$\frac{R}{\sqrt{R^{2} - ω^{2} L^{2}}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

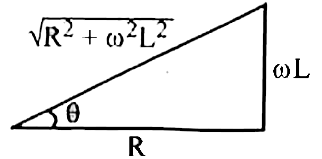
$tan θ = \frac{ω L}{R}$
$∴$ Power factor = $cos θ = \frac{R}{\sqrt{R^{2} + L^{2} ω^{2}}}$

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROMAGNETIC INDUCTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
200 $Ω$ resistance and 1H inductance are connected in series with an A.C. circuit. The frequency of the source is $\frac{200}{2 π}$ Hz. Then phase difference in between V and I will be-
A $30^{\circ}$
B $60^{\circ}$
C $45^{\circ}$
D $90^{\circ}$
Question 2 - Select One
In an A.C. circuit, a resistance $R = 40 Ω$ and an inductance L are connected in series. If the phase angle between voltage and current is $45^{\circ}$ , then the value of the inductive reactance will be
A $20 Ω$
B $40 Ω$
C $10 Ω$
D $50 Ω$
Question 3 - Select One
The impedance of a circuit, when a resistance R and an inductor of inductance are connected in series in an AC circuit of frequency f is
A $\sqrt{R + 2 π^{2} f^{2} L^{2}}$
B $\sqrt{R + 4 π^{2} f^{2} L^{2}}$
C $\sqrt{R^{2} + 4 π^{2} f^{2} L^{2}}$
D $\sqrt{R^{2} + 2 π^{2} f^{2} L^{2}}$

MARVEL PUBLICATION-ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTS -TEST YOUR GRASP - 16

Home
Ask Doubt
Profile