A long straight wire carries a current of 2A. An electron travels with a velocity of 4×104ms−1 parallel to the wire 0⋅1mm from it, and in a direction opposite to the current. What force does the magnetic field of current exert on the moving electron. Charge on electron =1⋅6×10−19C.
The correct Answer is:2⋅56×10−20N, towards the conductor
To solve the problem, we will follow these steps:
Step 1: Calculate the Magnetic Field (B) due to the Current-Carrying Wire
The formula for the magnetic field around a long straight wire carrying current I at a distance d is given by:
B=μ0I2πd
Where:
- μ0=4π×10−7T m/A (permeability of free space)
- I=2A (current in the wire)
- d=0.1mm=0.1×10−3m=1×10−4m
Substituting the values:
B=4π×10−7×22π×1×10−4=8×10−72×10−4=4×10−3T
Step 2: Determine the Direction of the Magnetic Field
Using the right-hand rule, if the current is flowing in one direction, the magnetic field circles around the wire. Since the electron is moving opposite to the current, the magnetic field at the position of the electron will be directed out of the plane (positive k-direction).
Step 3: Calculate the Force (F) on the Electron
The force on a charged particle moving in a magnetic field is given by:
F=q(v×B)
Where:
- q=−1.6×10−19C (charge of the electron)
- v=4×104m/s (velocity of the electron)
- B=4×10−3T (magnetic field calculated above)
Step 4: Determine the Velocity and Magnetic Field Vectors
Assuming the electron is moving in the negative x-direction:
→v=−4×104^im/s
→B=4×10−3^kT
Step 5: Calculate the Cross Product v×B
Using the determinant method for the cross product:
→F=q→v×→B=−1.6×10−19^q⋅∣∣
∣
∣∣^i^j^k−4×10400004×10−3∣∣
∣
∣∣
Calculating the determinant:
→v×→B=^i(0⋅4×10−3−0)−^j(−4×104⋅4×10−3−0)+^k(0−0)
=0^i+0^j+(−4×104⋅4×10−3)^j
=16^j(in the positive y-direction)
Step 6: Calculate the Force Magnitude and Direction
Now substituting back into the force equation:
F=−1.6×10−19⋅16=−2.56×10−18N
The negative sign indicates that the force is in the negative y-direction.
Final Answer
The force exerted on the moving electron by the magnetic field of the current is:
F=2.56×10−18N(in the negative y-direction)
---
The formula for the magnetic field around a long straight wire carrying current I at a distance d is given by:
- μ0=4π×10−7T m/A (permeability of free space)
- I=2A (current in the wire)
- d=0.1mm=0.1×10−3m=1×10−4m
Using the right-hand rule, if the current is flowing in one direction, the magnetic field circles around the wire. Since the electron is moving opposite to the current, the magnetic field at the position of the electron will be directed out of the plane (positive k-direction).
The force on a charged particle moving in a magnetic field is given by:
- q=−1.6×10−19C (charge of the electron)
- v=4×104m/s (velocity of the electron)
- B=4×10−3T (magnetic field calculated above)
Assuming the electron is moving in the negative x-direction:
→B=4×10−3^kT
Using the determinant method for the cross product:
∣
∣∣^i^j^k−4×10400004×10−3∣∣
∣
∣∣
=0^i+0^j+(−4×104⋅4×10−3)^j
=16^j(in the positive y-direction)
Now substituting back into the force equation:
The force exerted on the moving electron by the magnetic field of the current is:
Topper's Solved these Questions
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:PRADEEPChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Test Your Grip (a)
Explore 1 Video
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:PRADEEPChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Test Your Grip (c)
Explore 1 Video
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:PRADEEPChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Value Based Questions
Explore 2 Videos
- ELECTROSTATICSBook:PRADEEPChapter:ELECTROSTATICSExercise:ASSERTION-REASON TYPE QUESTIONS
Explore 2 Videos
- OPTICSBook:PRADEEPChapter:OPTICSExercise:Multiple choice questions
Explore 1 Video
Similar Questions
A long straight wire AB carries a current of 4A. A proton P travels at 4×106ms−1 parallel to the wire, 0⋅2m from it and in a direction opposite to the current as shown in figure. Calculate the force which the magnetic field of current exerts on the proton. Also specify the direction of the force.
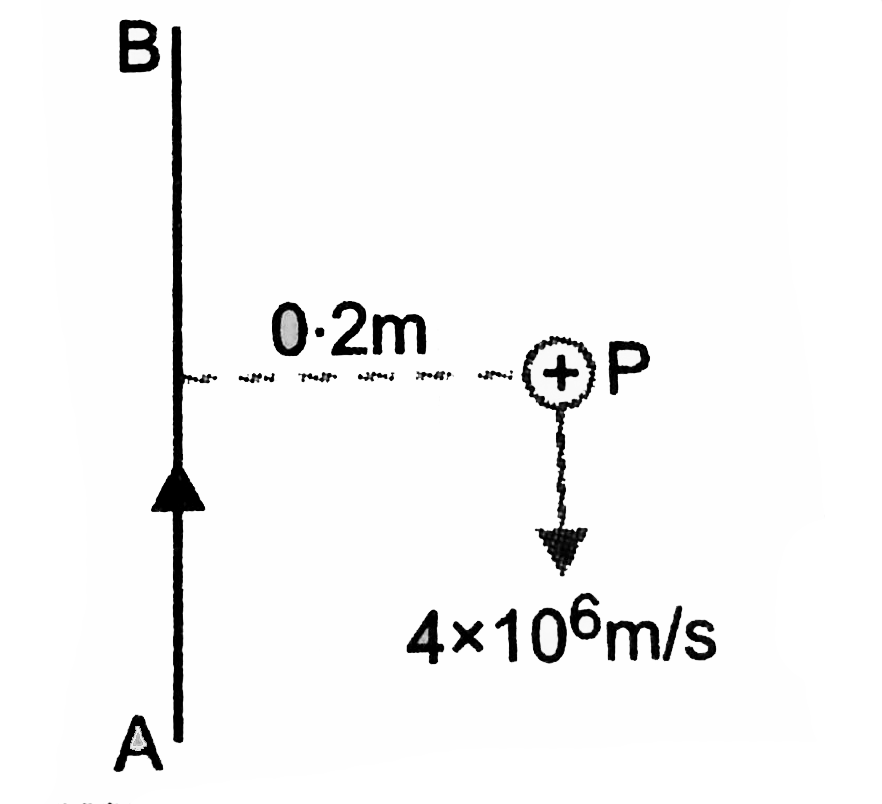
View SolutionA long straight wire AB carries a current of 4 A. A proton P travels at 4×106ms−1 parallel to the wire 0.2 m from it and in a direction opposite to the current as shown in the figure. Calculate the force which the magnetic field due to the current carrying wire exerts on the proton. Also specify its direction.
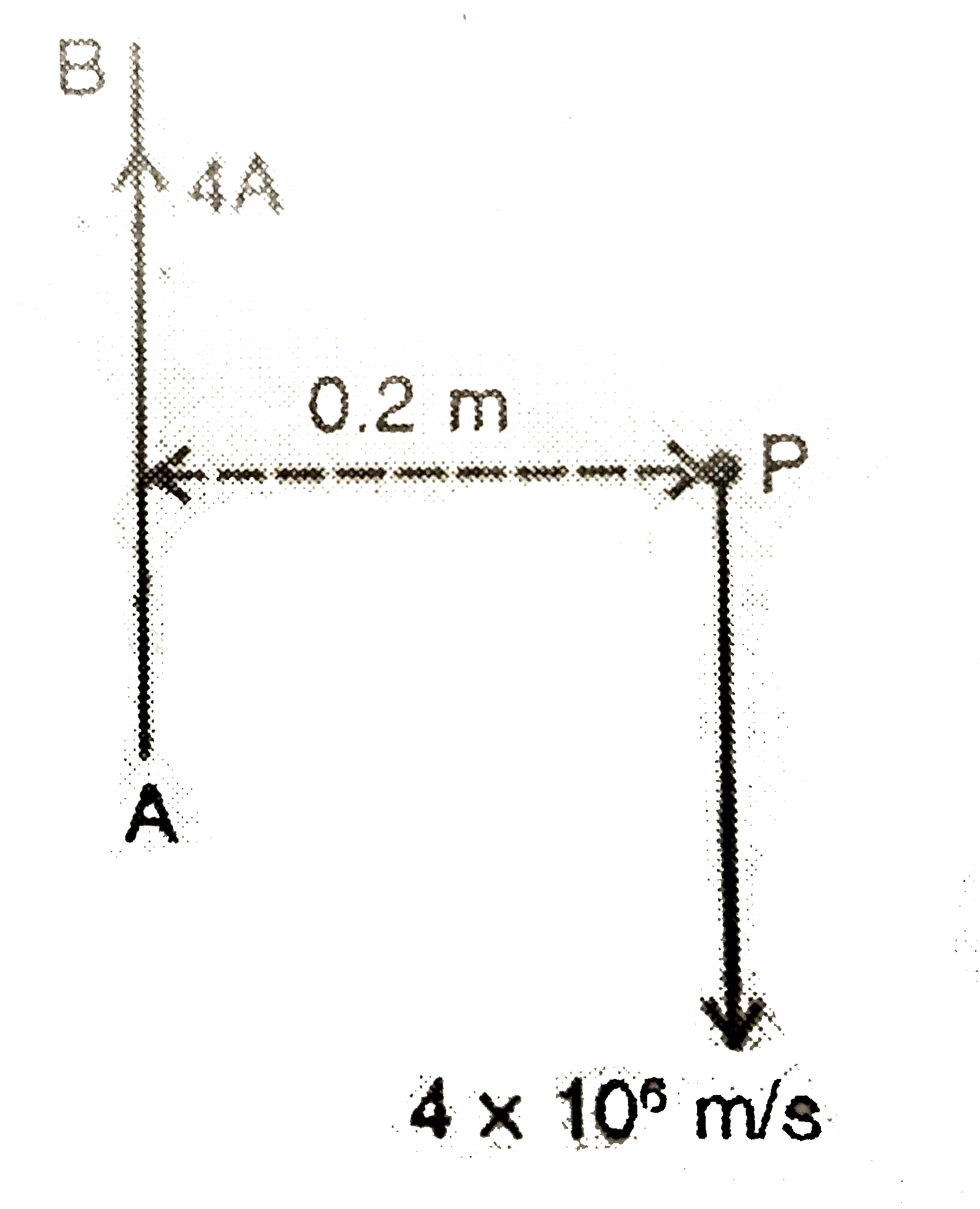
View Solution
Knowledge Check
A straight conductor carries a current of 5A. An electron travelling with a speed of 15×106ms−1 parallel to the wire at a distance of 0.1m from the conductor, experiences a force of
A8×10−20NB3.2×10−19NC8×10−18ND1.6×10−19NA long straight wire carries a current of 50 A. An electron moving at 107 m/s is 5 cm away from the wire. The force acting on electron if its velocity is directed towards the wire will be
A1.6×10−6 NB3.2×10−16 NC4.8×10−16 ND1.8×10−16 NA long straight wire carries a current of 10 A. An electron travels perpendicular to the plane of this wire at a distance 0.1 m with a velocity of 5.0×106m/s. What is the force acting on the electron due to the current in wire ?
A2.2×10−17NB1.6×10−17NC0.6×10−17NDZero
A long straight wire AB carries a current of 4 A. A proton P travels at 4×106ms−1 parallel to the wire 0.2 m from it and in a direction opposite to the current as shown in the fig. Calculate the force which the magnetic field due to the current carrying wire exerts on the proton. Also specify its direction.

View SolutionA long straight wire carrying a current of 25A is placed in an external uniform magnetic field 3⋅0×10−4T parallel to the current. Find the magnitude of the resultant magnetic field at a point 1⋅5cm away from the wire.
View SolutionA long straight wire carrying a current of 20A is placed in an external uniform magnetic field of 3×10−4T parallel to the current. Find the magnitude of resultant field at a point 2⋅0cm away from the wire.
View SolutionA straight wire carries a current of 10A. An electron moving at 103 m/s is at distance 2.0 cm from the wire. Find the force acting on the electron if its velocity is directed toward the wire?
View SolutionA long wire carries a current of 5A. An electron at a distance of 50 cm from this wire is moving with a speed of 107 m/s What is the force acting on the electron, when it moves directly towards the wire ?
View Solution

