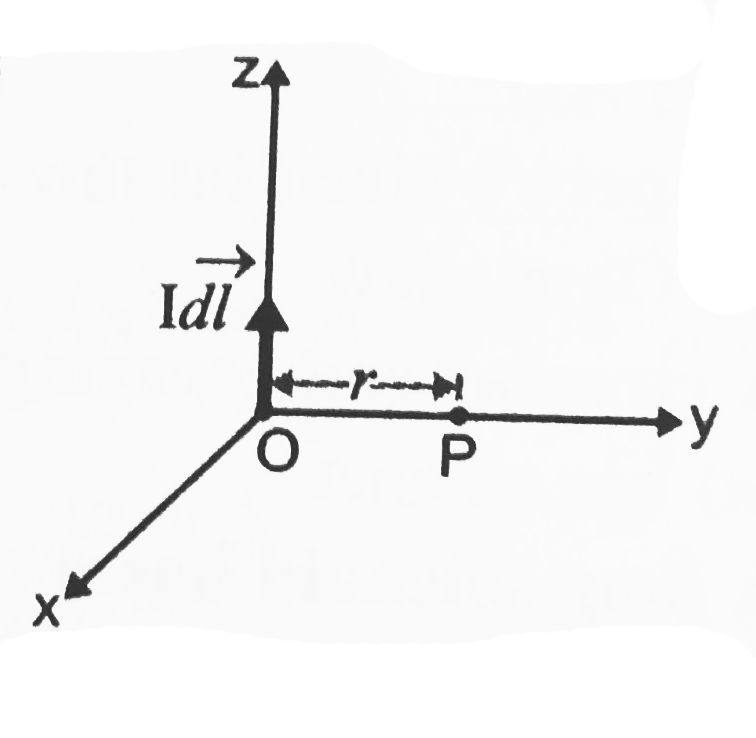
State Biot Savart's law. A current I flows in a conductor placed perpendicular to the plane of paper. Indicate the direction of the magnetic field due to a small element at a point P at a distance from the element as shown in figure.

According to Biot-Savart's law, the magnitude of the magnetic field induction at a point P, due to current element of length , carrying current I, at a distance r from the element is given by
The direction of is perpendicular to the plane containing and and is directed along x-axis, which is given by Right Hand Rule.
Topper's Solved these Questions
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Conceptual Problems (d)
2 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Very Short Answer Questions (a)
2 Videos
- ELECTROSTATICSBOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - ASSERTION-REASON TYPE QUESTIONS
2 Videos
- OPTICSBOOK - PRADEEPCHAPTER - OPTICSEXERCISE - Multiple choice questions
1 Videos
Similar Questions
A current I flows in a conductor placed perpendicular to the plate of the paper. Indicate the direction of the magnetic field due to a small element d→l at point P situated at a distance →r from the element as shown in the figure.
View SolutionState Biot-Savart law.
A current I flows in a conductor placed perpendicular to the plane of the paper. Indicate the direction of the magnetic field due to a small element →dl at point P situated at a distance →r from the element as shown in figure.
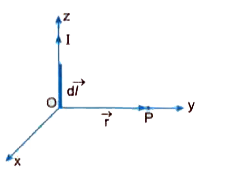
View Solution
Knowledge Check
The magnetic field d→B due to a small current element d→l at a distance →r and element carrying current i is,
Ad→B=μ04πi(d→l×→rr)Bd→B=μ04πi2(d→l×→rr)Cd→B=μ04πi2(d→l×→rr2)Dd→B=μ04πi(d→l×→rr3)The magnetic field −→dB due to a small current element →dl carrying a current I at a distance →r is given as
A−→dB=μ04πI⎡⎣−→dI×→rr⎤⎦B−→dB=μ04πI2⎡⎣→dl×→rr⎤⎦C−→dB=μ04πI2⎡⎣→dl×→rr2⎤⎦D−→dB=μ04πI⎡⎣→dl×→rr3⎤⎦The magnetic field ¯¯¯¯¯dB due to a small current element ¯¯¯dl at a distance →r and carrying current 'I' is
A¯¯¯¯¯dB=μ04πi(¯¯¯dlׯrr)B¯¯¯¯¯dB=μ04πi2(¯¯¯dlׯrr2)C¯¯¯¯¯dB=μ04πi2(¯¯¯dlׯrr)D¯¯¯¯¯dB=μ04πi(¯¯¯dlׯrr3)
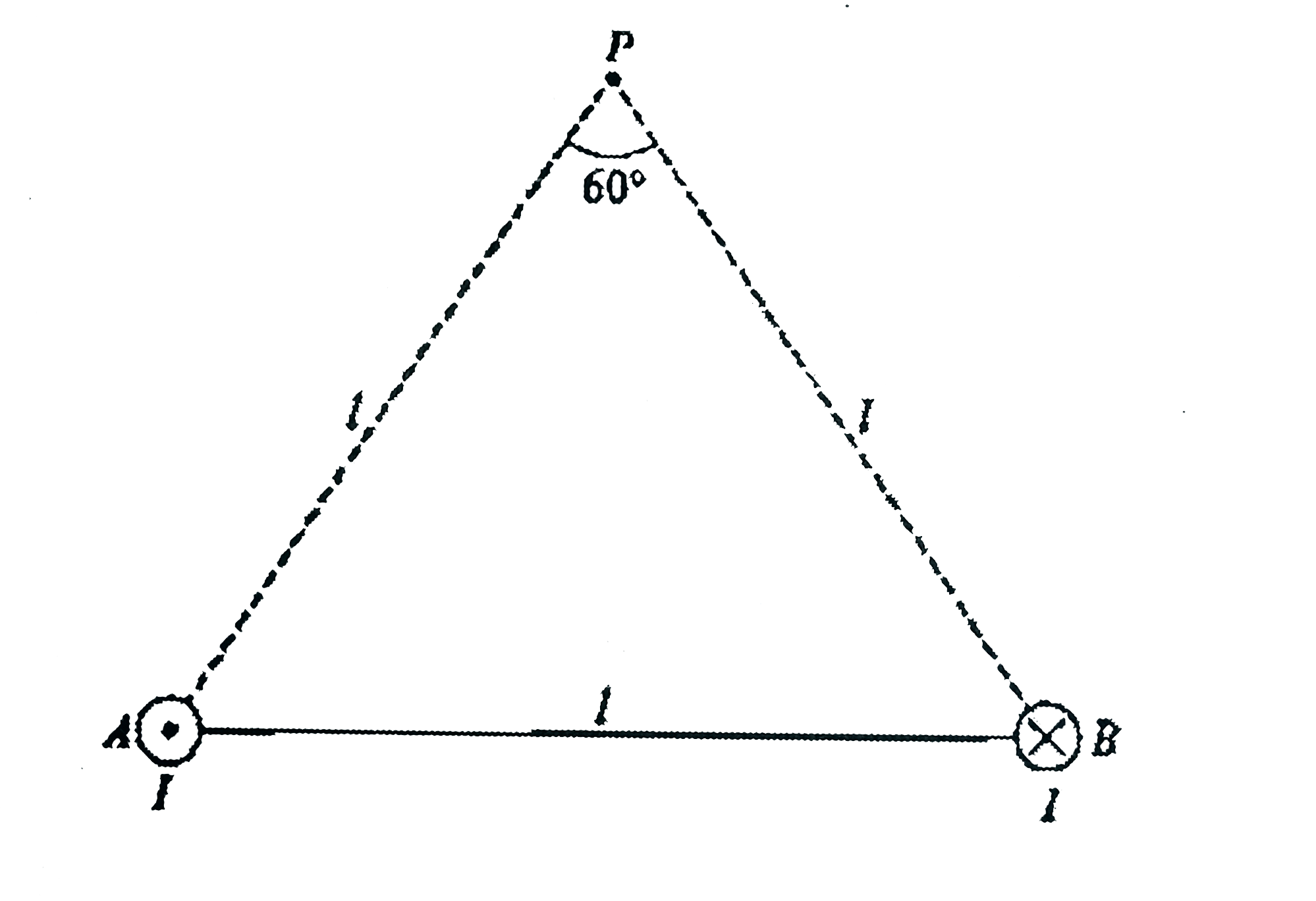
figure 4.22 shows two long wires A and B, each carrying a current I, separated by a distance l and oriented in a plane perpendicular to the plane of paper. The directions of currents are shown in figure. Find the magnetic induction at a point P located at a distance l from both wires as shown in figure4.22
View SolutionThe magnetic field at the origin due to a current element I (→dl)placedataposi→n(→r)is
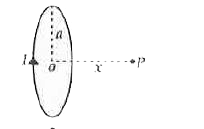
View SolutionThe magnetic field at a point P due to a current carrying coil as shown in figure is
View SolutionA current flows in a conductor from east to west. The direction of the magnetic field at a points above the conductor is
View SolutionThe magnetic field (d→B) at a point due to an elemental conductor (d→l) carrying a current (i) at a distance (→r) from the elemetn, is given by
View Solution
