The magnetic field (d→B) at a point due to an elemental conductor (d→l) carrying a current (i) at a distance (→r) from the elemetn, is given by
Faraday's Law
Columb's Law
Biot-Savart's Law
Ampere's Law
The correct Answer is:C
Step by step video, text & image solution for The magnetic field (d vecB) at a point due to an elemental conductor (d vecl) carrying a current (i) at a distance (vecr) from the elemetn, is given by by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MAGNETIC EFFECT OF ELECTRIC CURRENT BOOK - MARVEL PUBLICATIONCHAPTER - MAGNETIC EFFECT OF ELECTRIC CURRENT EXERCISE - MCQ (HIGHER LEVEL)
3 Videos
- MAGNETIC EFFECT OF ELECTRIC CURRENT BOOK - MARVEL PUBLICATIONCHAPTER - MAGNETIC EFFECT OF ELECTRIC CURRENT EXERCISE - MCQ (STANDARD LEVEL)
46 Videos
- FRICTIONAL IN SOLIDS AND LIQUIDS BOOK - MARVEL PUBLICATIONCHAPTER - FRICTIONAL IN SOLIDS AND LIQUIDS EXERCISE - TEST YOUR GRASP
10 Videos
- MAGNETISMBOOK - MARVEL PUBLICATIONCHAPTER - MAGNETISMEXERCISE - TEST YOUR GRASP
10 Videos
Similar Questions
Write using Biot-Savart law, the expression for the magnetic field →B due to an element →dl carrying current I at a distance →r from it in vector form. Hence, derive the expression for the magnetic field due to a current loop of radius R at a point P distant x from its centre along the aixs of the loop.
View SolutionWrite the relation for the magnetic field induction at a point due to a linear conductor carrying current and hence deduce the relation for the magnetic field induction at a point due to a very long linear conductor carrying current.
View Solution
Knowledge Check
The magnetic field at a point due to a current carrying conductor is directly proportional to
Aresistance of the conductorBthickness of the conductorCdistance from the conductorDcurrent flowing through the conductorThe magnetic field −→dB due to a small current element →dl carrying a current I at a distance →r is given as
A−→dB=μ04πI⎡⎣−→dI×→rr⎤⎦B−→dB=μ04πI2⎡⎣→dl×→rr⎤⎦C−→dB=μ04πI2⎡⎣→dl×→rr2⎤⎦D−→dB=μ04πI⎡⎣→dl×→rr3⎤⎦Magnetic field at a point on the line of current carrying conductor is
AmaximumBinfinityCzeroDfinite value
(a) State Bio-Savart's law in vector form expressing the magnetic field due to an element →dl carrying current I at a distance r from the element.
(b) Write the expression for the magnitude of the magnetic field at the centre of a circular loop of radius 'R' carrying a steady current I. Draw the field lines due to the current loop.
View SolutionFind the magnetic field at a point P on the perpendicular bisector of the current carrying conductor :-
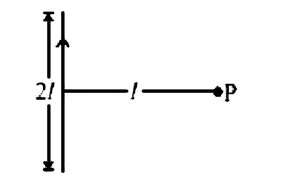
View SolutionThe magnetic induction due to an infinitely long straight wire carrying a current i at a distance r from wire is given by
View SolutionThe magnetic field d→B due to a small current element d→l at a distance →r and element carrying current i is,
View SolutionThe magnetic field ¯¯¯¯¯dB due to a small current element ¯¯¯dl at a distance →r and carrying current 'I' is
View Solution
