A concave mirrorr of focal length f1 is placed at a distance of d from a convex lens of focal length f2. A beam of light coming from infinity and falling on this convex lens-concave mirrorr combination returns to infinity. The distance d must equal.
f1+f2
−f1+f2
2f1+f2
−2f1+f2
The correct Answer is:C
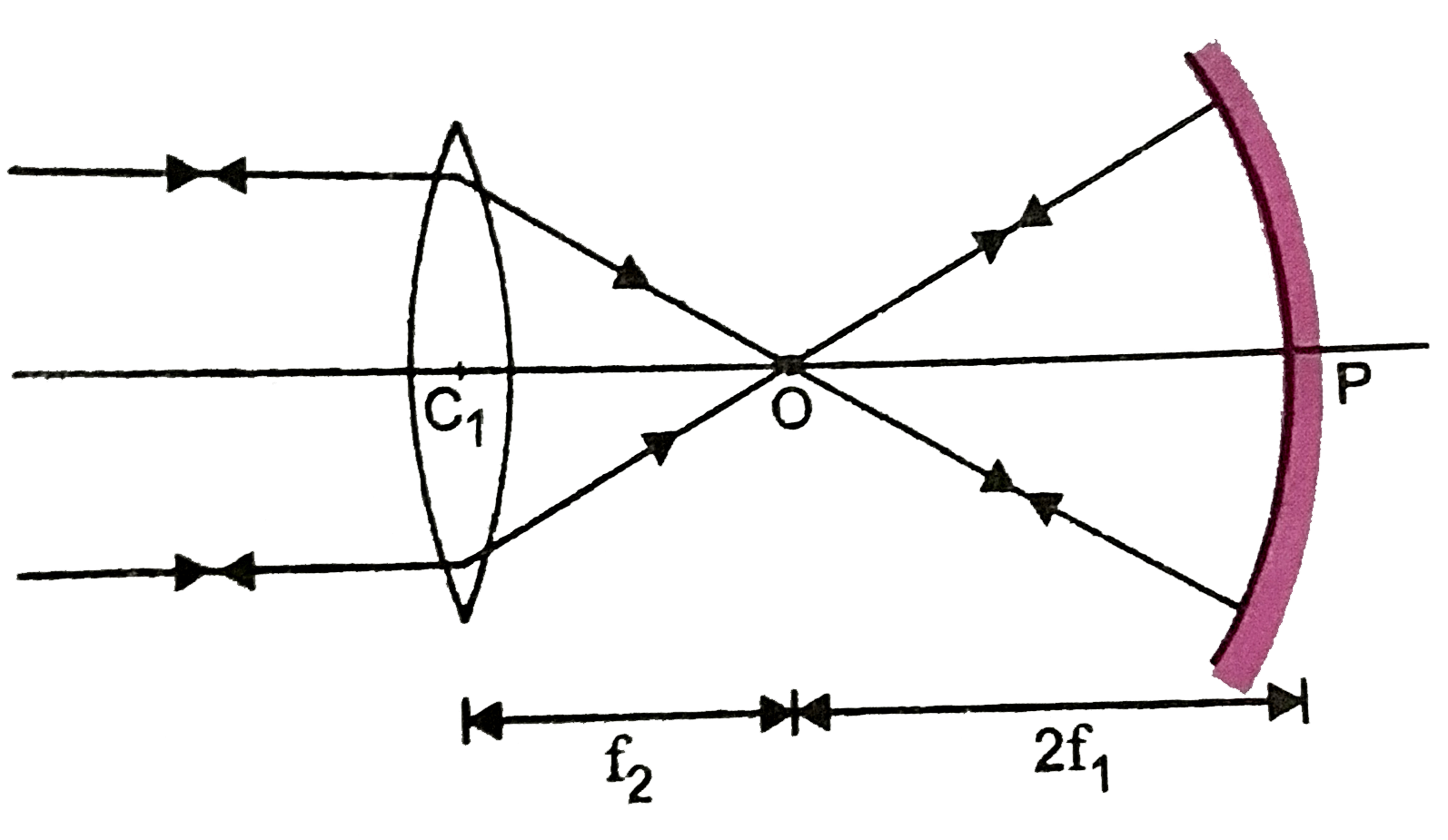
In Fig.,
focal length of concave mirror =f1 and focal length of convex lens =f2
A beam of light coming from infinity and falling on convex lens. Therefore, C1O=f2. The rays of light from O will retrace their path on reflection from concave mirror only when O is at centre of curvature of concave mirror, i.e., OP=R=2f1.
∴C1P=d=C1O+OP=(f2+2f1).
 .
.
Topper's Solved these Questions
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:(Competition)Comprehension
Explore 7 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Integer Question
Explore 4 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:(Exemplar) Multiple choice
Explore 16 Videos
- PROPERTIES OF BULK MATTERBook:PRADEEPChapter:PROPERTIES OF BULK MATTERExercise:Multiple choice questions
Explore 7 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:Assertion- Reason Type questions
Explore 20 Videos
Similar Questions
Power (P) of a lens is given by reciprocal of focal length (f) of the lens. i.e. P=1/f. When f is in metre, P is in dioptre. For a convex lens, power is positive and for a concave lens, power is negative. When a number of thin lenses of powers p1,p2,p3.... are held in contact with one another, the power of the combination is given by algebraic sum of the powers of all the lenses
i.e., P=p1+p2+p3+........
Answer the following questions :
Focal length of the combined three lenses would be
View SolutionA man wants to distinguish between two pillars located at a distance of 11km. What should be the minimum distance between the pillars ?
View SolutionA ray of light incident at an angle θ on a refracting face of a prism emerges from the other face normally. If the angle of the prism is 5∘ and the prism is made of a material of refractive index 1.5, the angle of incidence is.
View SolutionIn the experiment to determine Young's modulus of the material of a wire under tension
used in the arrangement as shown. The percentage error in the measurement
of length is a in the measurement of the radius of the wire is b and in the
measurement of the change in length of the wire is c. Percentage error in the measurement
of Young's modulus for a given load is

View SolutionAssertion : In rolling, all points of a rigid body have the same linear velocity.
Reason : The rotational motion does not affect the linear velocity.
View SolutionA diverging lens of focal length f1 is placed in front of and coaxially with a concave mirror of foacl length f2. Their separation is d. A parallel beam of light incident on the lens returns as a parallel beam from the arrangement. Then,
View SolutionA converging lens of focal length f_(1) is placed in front of and coaxially with a convex mirror of focal length f_(2) . Their separation is d. A parallel beam of light incident on the lens returns as a parallel beam from the arrangement, Then,
View SolutionAn object is placed at a distance 2f from a concave mirror of focal length f. Light reflected from the mirror falls on a plane mirror. The distance of the plane mirror from the concave mirror equals f. The distance of the final image (due to reflection at both concave and plane mirror) from the concave mirror is
View SolutionA concave mirrorr of focal length f_(1) is placed at a distance of d from a convex lens of focal length f_(2) . A beam of light coming from infinity and falling on this convex lens-concave mirrorr combination returns to infinity. The distance d must equal.
View SolutionWe combined a convex lens of focal length f1 and concave lens of focal lengths f2 and their combined focal length was F . The combination of these lenses will behave like a concave lens, if
View SolutionRay coming from an object situated at infinity, fall on a convex lens and an image is formed at a distance of 16 cm from the lens. When a concave lens is kept in contact with the convex lens, the image is formed at a distance of 20 cm from the lens combination. Calculate the focal length of the concave lens.
View SolutionA convex lens of focal length f1 is kept in contact with a concave lens of focal length f2. Find the focal length of the combination.
View SolutionA convex lens of focal length f_(1) is kept in contact with a concave lens of focal length f_(2) . Find the focal length of the combination.
View SolutionA concave mirrorr of focal length f_(1) is placed at a distance of d from a convex lens of focal length f_(2) . A beam of light coming from infinity and falling on this convex lens-concave mirrorr combination returns to infinity. The distance d must equal.
View SolutionWe combined a convex lens of focal length f_(1) and concave lens of focal lengths f_(2) and their combined focal length was F . The combination of these lenses will behave like a concave lens, if
View SolutionA diverging lens of focal length f1 is placed in front of and coaxially with a concave mirror of foacl length f2. Their separation is d. A parallel beam of light incident on the lens returns as a parallel beam from the arrangement. Then,
View Solution

