One face of prism of refracting angle 30∘ and refractive index 1.414 is silvered. At what angle must a ray of light fall on the unsilvered face so that it retraces its path out of the prism ?
The correct Answer is:45∘
To solve the problem, we need to determine the angle at which a ray of light must strike the unsilvered face of a prism with a refracting angle of 30∘ and a refractive index of 1.414 (which is √2), such that it retraces its path after reflecting off the silvered face.
1. Understanding the Geometry of the Prism:
- The prism has a refracting angle A=30∘.
- One face of the prism is silvered, which means it acts as a mirror.
2. Identifying the Angles:
- Let R1 be the angle of incidence at the silvered face.
- Let R2 be the angle of refraction as the ray enters the prism.
- According to the prism's geometry, we have:
R1+R2=A
- Since A=30∘, we can write:
R1+R2=30∘
3. Using Snell's Law:
- Snell's law states:
n1sinI=n2sinR
- Here, n1=1 (the refractive index of air), n2=1.414 (the refractive index of the prism), I is the angle of incidence, and R is the angle of refraction.
- For the ray entering the prism:
sinI=1.414sinR2
4. Finding the Relationship Between Angles:
- From the previous step, we know:
R1=30∘−R2
- Substituting this into Snell's law gives:
sinI=1.414sin(30∘−R1)
5. Considering the Reflection:
- For the ray to retrace its path, it must reflect off the silvered face at an angle equal to R1 (which is the angle of incidence).
- The angle of incidence at the silvered face must equal the angle of reflection, which is also R1.
6. Finding the Angle of Incidence:
- Since R2=0∘ when the ray retraces its path, we have:
R1=30∘
- Thus, we can apply Snell's law again:
sinI=1.414sin(30∘)
- We know sin(30∘)=12:
sinI=1.414×12=1.4142
7. Calculating the Angle of Incidence:
- Therefore:
sinI=1.4142=0.707
- Taking the inverse sine:
I=sin−1(0.707)=45∘
Final Answer:
The angle at which the ray of light must fall on the unsilvered face of the prism is 45∘.
- The prism has a refracting angle A=30∘.
- One face of the prism is silvered, which means it acts as a mirror.
- Let R1 be the angle of incidence at the silvered face.
- Let R2 be the angle of refraction as the ray enters the prism.
- According to the prism's geometry, we have:
R1+R2=A
- Since A=30∘, we can write:
R1+R2=30∘
- Snell's law states:
n1sinI=n2sinR
- Here, n1=1 (the refractive index of air), n2=1.414 (the refractive index of the prism), I is the angle of incidence, and R is the angle of refraction.
- For the ray entering the prism:
sinI=1.414sinR2
- From the previous step, we know:
R1=30∘−R2
- Substituting this into Snell's law gives:
sinI=1.414sin(30∘−R1)
- For the ray to retrace its path, it must reflect off the silvered face at an angle equal to R1 (which is the angle of incidence).
- The angle of incidence at the silvered face must equal the angle of reflection, which is also R1.
- Since R2=0∘ when the ray retraces its path, we have:
R1=30∘
- Thus, we can apply Snell's law again:
sinI=1.414sin(30∘)
- We know sin(30∘)=12:
sinI=1.414×12=1.4142
- Therefore:
sinI=1.4142=0.707
- Taking the inverse sine:
I=sin−1(0.707)=45∘
The angle at which the ray of light must fall on the unsilvered face of the prism is 45∘.
Topper's Solved these Questions
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Problem For Practice(d)
Explore 35 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:(Test Your Grip)Multiple Choice (b)
Explore 10 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Problem For Practice(b)
Explore 66 Videos
- PROPERTIES OF BULK MATTERBook:PRADEEPChapter:PROPERTIES OF BULK MATTERExercise:Multiple choice questions
Explore 7 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:Assertion- Reason Type questions
Explore 20 Videos
Similar Questions
The face AC of the prism ABC of refracting angle 30∘ and refractive index square root 2 is silvered. A ray of light, after refraction from face AB, strike the face AC at 90∘. Find the angle of incidence and path traced by the ray after reflecting from the silvered surface.
View SolutionA prism of flint galss with an angle of refraction of 30 is placed in water. At what angle should a ray, of light fall on face of the prism so that inside the prism the ray is perpendicular to the bisector of the angle of refraction? Through what angle will the ray turn after passing through both faces of the prism?
View Solution
Knowledge Check
Angle of prism is 30∘ and its refractive index is √2 . One of its surface is silvered. At what angle of incidence, a ray should be incident on one surface so that after reflection from the silvered surface, it retraces its path?
A30∘B60∘C45∘Dsin−1(0.15)The angle of minimum deviation is an equilateral prism of refractive index 1.414 is
A60∘B30∘C90∘D45∘Angle of a prism is 30∘ and its refractive index is √2 and one of the surface is silvered At what angle of incidence a ray should be incident on one surface so that after reflection from the silvered surface it retraces its path
A30∘B60∘C45∘Dsin−1√1.5
State the conditions under which total internal reflection occurs. One face of a prism with a refracting angle of 30∘ is coated with silver. A ray incident on another face at an angle of 45∘ is refracted and reflected from the silver coated face and retraces its path. Find the refractive index of the material of the prism.
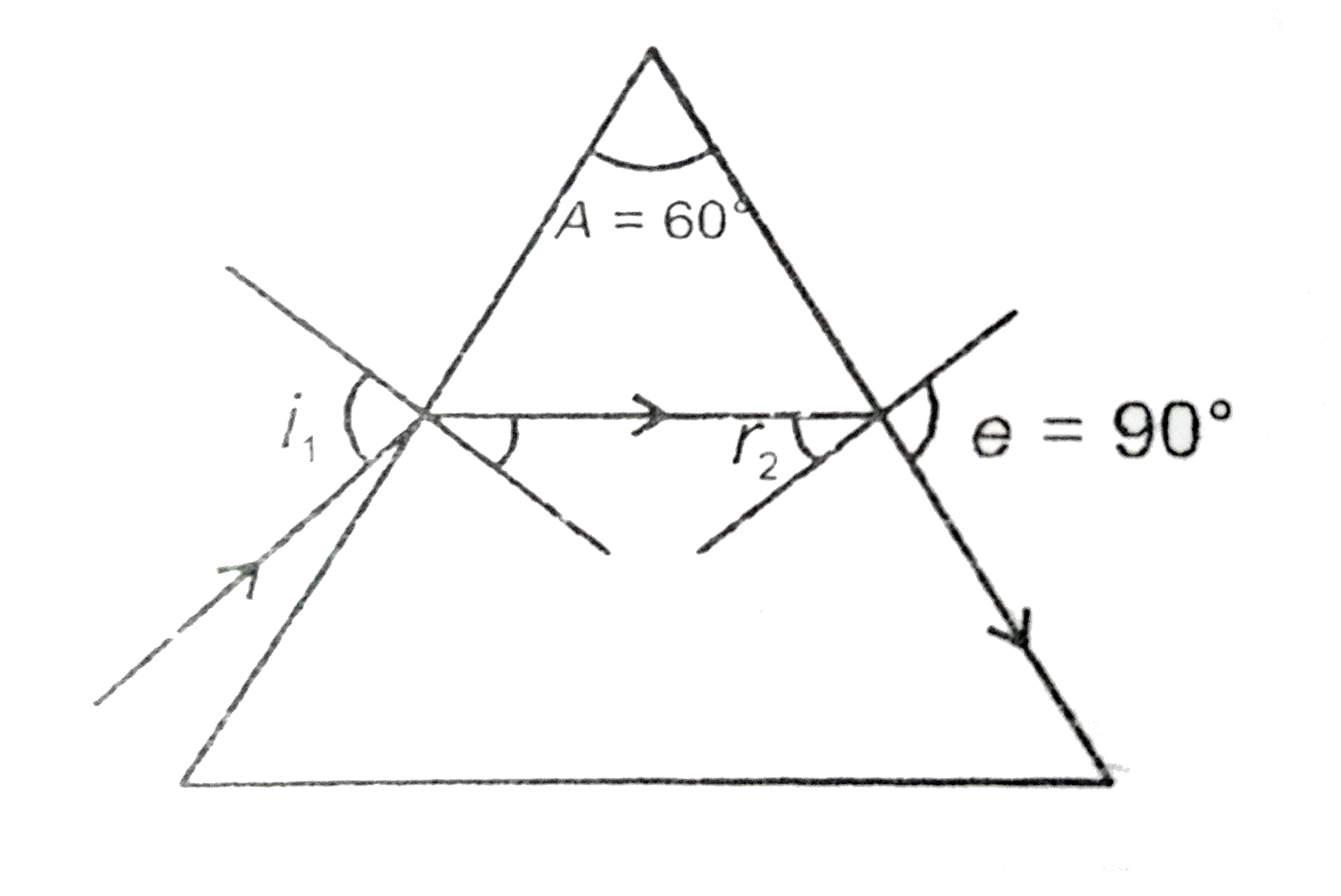
View SolutionCalculate the angle of incidence on the face of a prism of refracting angle 60∘ and of refractive index 1.5, for which the emergent ray just grazes the other face.
View SolutionOne face of a prism of refractive index 1.5 and angle 75∘ is covered with a liquid of refractive index 3√24. What should be the angle of incidence of light on the clear face of prism for which light is just totally refracted at the liquid covered face ?
View SolutionOne face of a prism of refractive index 1.5 and angle 75∘ is covered with a liquid of refractive index 3√24. What should be the angle of incidence of light on the clear face of prism for which light is just totally reflected at the liquid covered face ?
View SolutionAngle of a prism is 30∘ and its refractive index is √2 and one of the surface is silvered. At what angle of incidence, a ray should be incident on one surface so that after reflection from the silvered surface, it retraces its path ?
View Solution

