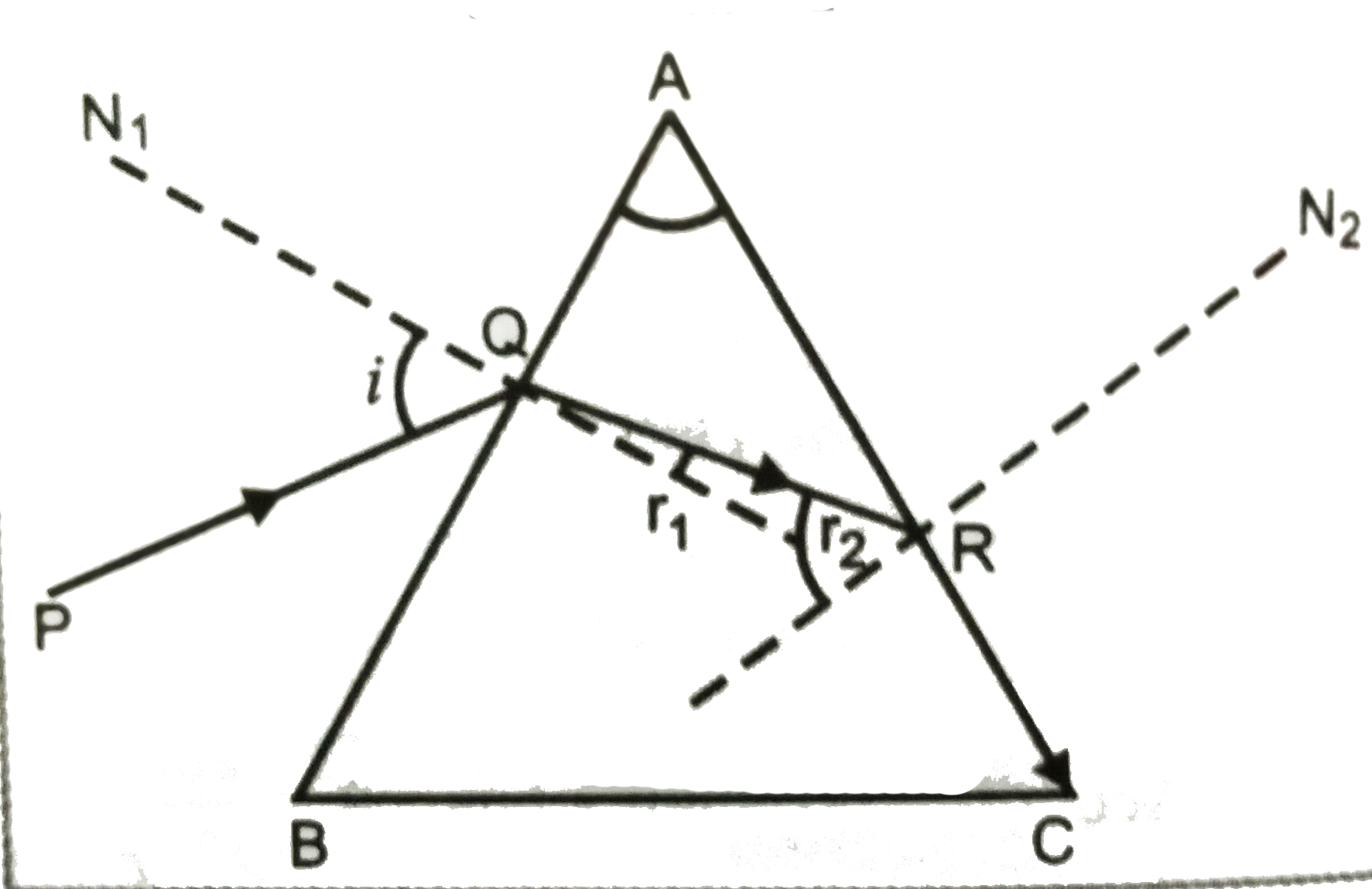
The refracting angle of a glass prism is 60∘ and μ of its material is 1.45. Calculate angle of incidence at the first that will just reflect internaly the ray at the second face.
The correct Answer is:24.2∘
Here, A=60∘,μ=1.45,i1=?
From μ=1sinC,
sinC=1μ=11.45=0.6897
C=sin−1(0.6897)=43.6∘
For total internal reflection at 2nd face of prism,
r2=C=43.6∘
From r1+mr2=A,
r1=A−r2=60∘−43.6∘=16.4∘
From μ=sini1sinr1,
sini1=μsinr1=1.45×sin16.4∘
=1.45×0.2823=0.4093
∴i1=sin−1(0.4093)=24.2∘.
Topper's Solved these Questions
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Problem For Practice(d)
Explore 35 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:(Test Your Grip)Multiple Choice (b)
Explore 10 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Problem For Practice(b)
Explore 66 Videos
- PROPERTIES OF BULK MATTERBook:PRADEEPChapter:PROPERTIES OF BULK MATTERExercise:Multiple choice questions
Explore 7 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:Assertion- Reason Type questions
Explore 20 Videos
Similar Questions
The refracting angle of a glass prism is 30∘. A ray is incident onto one of the faces perpendicular to it. Find the angle δ between the incident ray and the ray that leaves the prism. The refractive index of glass is μ=1.5.
View SolutionA light rays is incident on a prism of prism angle A and refractive index μ. Show that the smallest value of the angle of incidence for which the reflected ray does not suffer total internal reflection at the second face, i.e. just comes out of it, is given by
i=sin−1[(μ2−1)1/2sinA−cosA].
View Solution
Knowledge Check
The angle of prism is 60∘ and its refractive index is 1.5. There will be no emergent light if the angle of incidence on the first face is
Aequal to 30∘Bless than 27∘Cmore than 30∘Dequal to 60∘A ray of light is incident on a refracting face of glass prism of refracting angle 30∘. If the ray emerges normally from the second refracting surface, the angle of incidence is refracting surface, the angle of incidence is
[aμg=1.5]Asin−1(0.6)Bsin−1(0.7)Csin−1(0.75)Dsin−1(0.8)A ray of light is incident at an angle of 60∘ on one face of a prism of angle 30∘. The ray emerging out of the prism makes an angle of 30∘ with the incident ray. The emergent ray is
A0∘B90∘C30∘D45∘
A ray of light falls on a glass plate of refractive index μ=1.5.
What is the angle of incidence of the ray if the angle between the reflected and
refracted rays is 90∘?
View SolutionA right angle prism(45∘−90∘−45∘) of refractive index n has a plane of refractive index n1(n1<n) cemented to its diagonal face. The assembly is in air. The ray is incident on AB.
_E01_161_Q01.png)
(i) Calculate the angle of incidence at AB for which the ray strikes the diagonal face at the critical angle .
(ii) Assuming n = 1.352 , calculate the angle of incidence at AB for which the refracted ray passes through the diagonal face undeviated.
View SolutionA ray of light enters the face AB of a glass prism of refractive index μ at an angle of incidence i. Find the value of i such that no ray emerges from the face AC of the prism, given angle of prism is A.
View SolutionA ray of light the face AB of a glass prism of refractive index μ at an angle of incidence i. Find the value of i such that no ray emerges from the face AC of the prism. Given angle of prism is A.
View SolutionA ray of monochromatic light is incident on one refracting face of a prism of angle 75∘. It passes thorugh the prism and is incident on the other face at the critical angle. If the refractive index of the material of the prism is √2, the angle of incidence on the first face of the prism is
View Solution

