A particle is executing simple harmonic motion with a time period . At time it is at its position of equilibium. The kinetice energy -time graph of the particle will look like

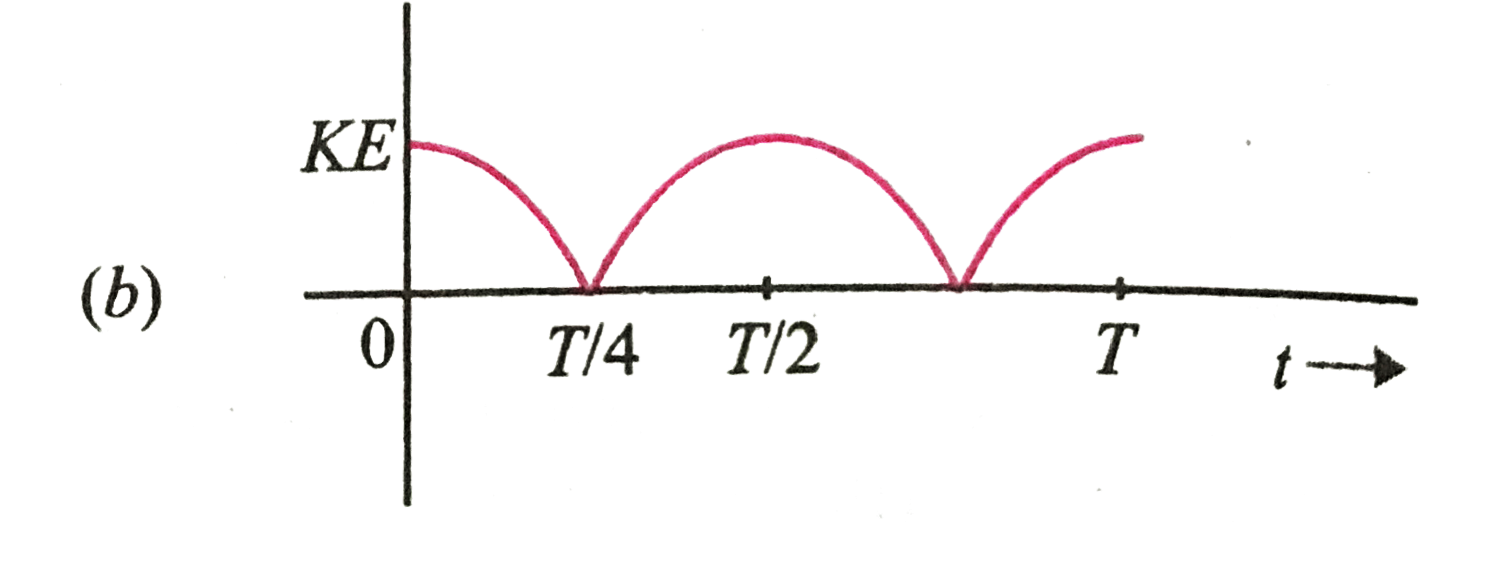

The correct Answer is:B
To solve the problem of determining the kinetic energy-time graph of a particle executing simple harmonic motion (SHM) with a time period T, we can follow these steps:
Step 1: Understand the Motion
The particle is executing SHM, which can be described by the equation:
y(t)=Asin(ωt+ϕ)
where A is the amplitude, ω is the angular frequency, and ϕ is the phase constant.
Step 2: Determine the Phase Constant
At time t=0, the particle is at its position of equilibrium, which means:
y(0)=0⟹Asin(ϕ)=0
Since A≠0, we have sin(ϕ)=0. This implies that ϕ=0 (since we consider the simplest case). Thus, the equation simplifies to:
y(t)=Asin(ωt)
Step 3: Find the Velocity
The velocity v(t) of the particle is the derivative of the displacement y(t) with respect to time:
v(t)=dydt=Aωcos(ωt)
Step 4: Calculate the Kinetic Energy
The kinetic energy KE of the particle is given by:
KE=12mv2=12m(Aωcos(ωt))2
This simplifies to:
KE=12mA2ω2cos2(ωt)
Step 5: Analyze the Kinetic Energy Function
The kinetic energy is proportional to cos2(ωt). The maximum value of KE occurs when cos2(ωt)=1 (i.e., when ωt=0,π,2π,…), and the minimum value occurs when cos2(ωt)=0 (i.e., when ωt=π2,3π2,…).
Step 6: Determine Key Points in the Cycle
- At t=0: KE is maximum.
- At t=T4: KE=0 (since cos2(π2)=0).
- At t=T2: KE is maximum again.
- At t=3T4: KE=0.
- At t=T: KE is maximum again.
Step 7: Sketch the Kinetic Energy-Time Graph
The graph of KE versus time will be a cosine squared function, oscillating between 0 and a maximum value, with maxima at t=0,T2,T and minima at t=T4,3T4.
Conclusion
The kinetic energy-time graph will look like a cosine squared wave, oscillating between 0 and its maximum value.
The particle is executing SHM, which can be described by the equation:
y(t)=Asin(ωt+ϕ)
where A is the amplitude, ω is the angular frequency, and ϕ is the phase constant.
At time t=0, the particle is at its position of equilibrium, which means:
y(0)=0⟹Asin(ϕ)=0
Since A≠0, we have sin(ϕ)=0. This implies that ϕ=0 (since we consider the simplest case). Thus, the equation simplifies to:
y(t)=Asin(ωt)
The velocity v(t) of the particle is the derivative of the displacement y(t) with respect to time:
v(t)=dydt=Aωcos(ωt)
The kinetic energy KE of the particle is given by:
KE=12mv2=12m(Aωcos(ωt))2
This simplifies to:
KE=12mA2ω2cos2(ωt)
The kinetic energy is proportional to cos2(ωt). The maximum value of KE occurs when cos2(ωt)=1 (i.e., when ωt=0,π,2π,…), and the minimum value occurs when cos2(ωt)=0 (i.e., when ωt=π2,3π2,…).
- At t=0: KE is maximum.
- At t=T4: KE=0 (since cos2(π2)=0).
- At t=T2: KE is maximum again.
- At t=3T4: KE=0.
- At t=T: KE is maximum again.
The graph of KE versus time will be a cosine squared function, oscillating between 0 and a maximum value, with maxima at t=0,T2,T and minima at t=T4,3T4.
The kinetic energy-time graph will look like a cosine squared wave, oscillating between 0 and its maximum value.
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBook:PRADEEPChapter:OSCILLATIONS AND WAVESExercise:integer type question
Explore 8 Videos
- OSCILLATIONS AND WAVESBook:PRADEEPChapter:OSCILLATIONS AND WAVESExercise:Assertion-Reason Type Questions
Explore 23 Videos
- OSCILLATIONS AND WAVESBook:PRADEEPChapter:OSCILLATIONS AND WAVESExercise:Multiple Choice Question-II
Explore 14 Videos
- MATHEMATICAL TOOLSBook:PRADEEPChapter:MATHEMATICAL TOOLSExercise:Fill in the blanks
Explore 5 Videos
- PHYSICAL WORLD AND MEASUREMENTBook:PRADEEPChapter:PHYSICAL WORLD AND MEASUREMENTExercise:Competiton Focus Jee Medical Entrance
Explore 18 Videos
Similar Questions
Knowledge Check
If a particle is executing simple harmonic motion, then acceleration of particle
Ais uniformBvaries linearly with timeCis non uniformDBoth (2) & (3)A particle executing simple harmonic motion with time period T. the time period with which its kinetic energy oscillates is
ATB2TC4TDT2A particle is executing simple harmonic motion .Its total energy is proportional to its -
Adisplacement from equilibrium positionBfrequency of oscillationCsquare of amplitude of motionDvelocity at equilibrium position
The displacement of a particle in simple harmonic motion in one time period is
View SolutionIf particle is excuting simple harmonic motion with time period T, then the time period of its total mechanical energy is :-
View SolutionA particle undergoes simple harmonic motion having time period T. The time taken in 3/8th oscillation is
View SolutionFor a particle executing simple harmonic motion, the amplitude is A and time period is T. The maximum speed will be
View SolutionA particle executing simple harmonic motion with an amplitude A. the distance travelled by the particle in one time period is
View Solution

