A simple pendulum of length L is suspended from the top of a flat beam of thickness L/2 . The bob is pulled away from the beam so that it makes an angle θ<30∘ with the vertical , as shown in figure. It is then released from rest. If ϕ is the maximum angular deflection to teh right, then
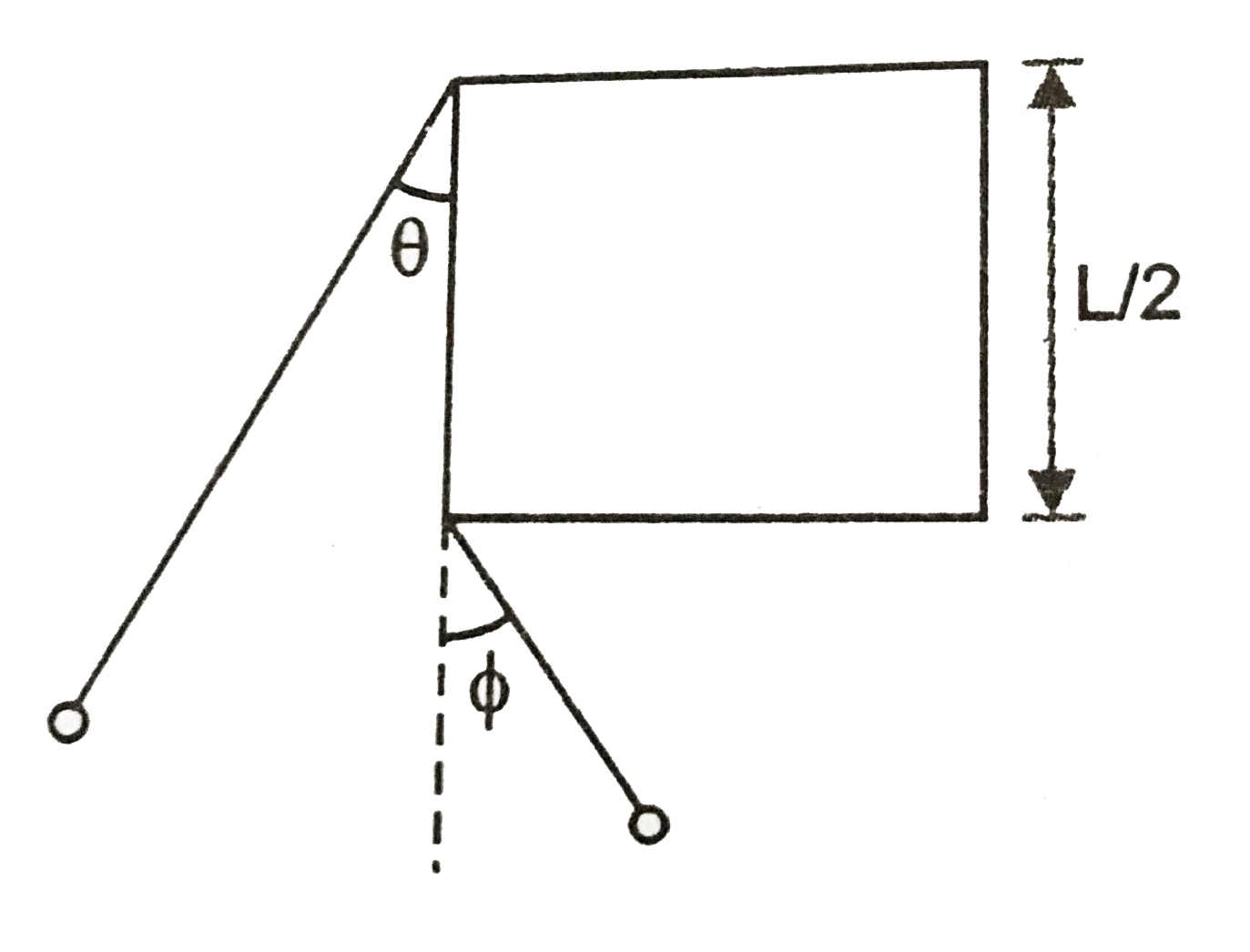
ϕ=θ
ϕ≥2θ
ϕ<θ
θ<ϕ<2θ
The correct Answer is:D
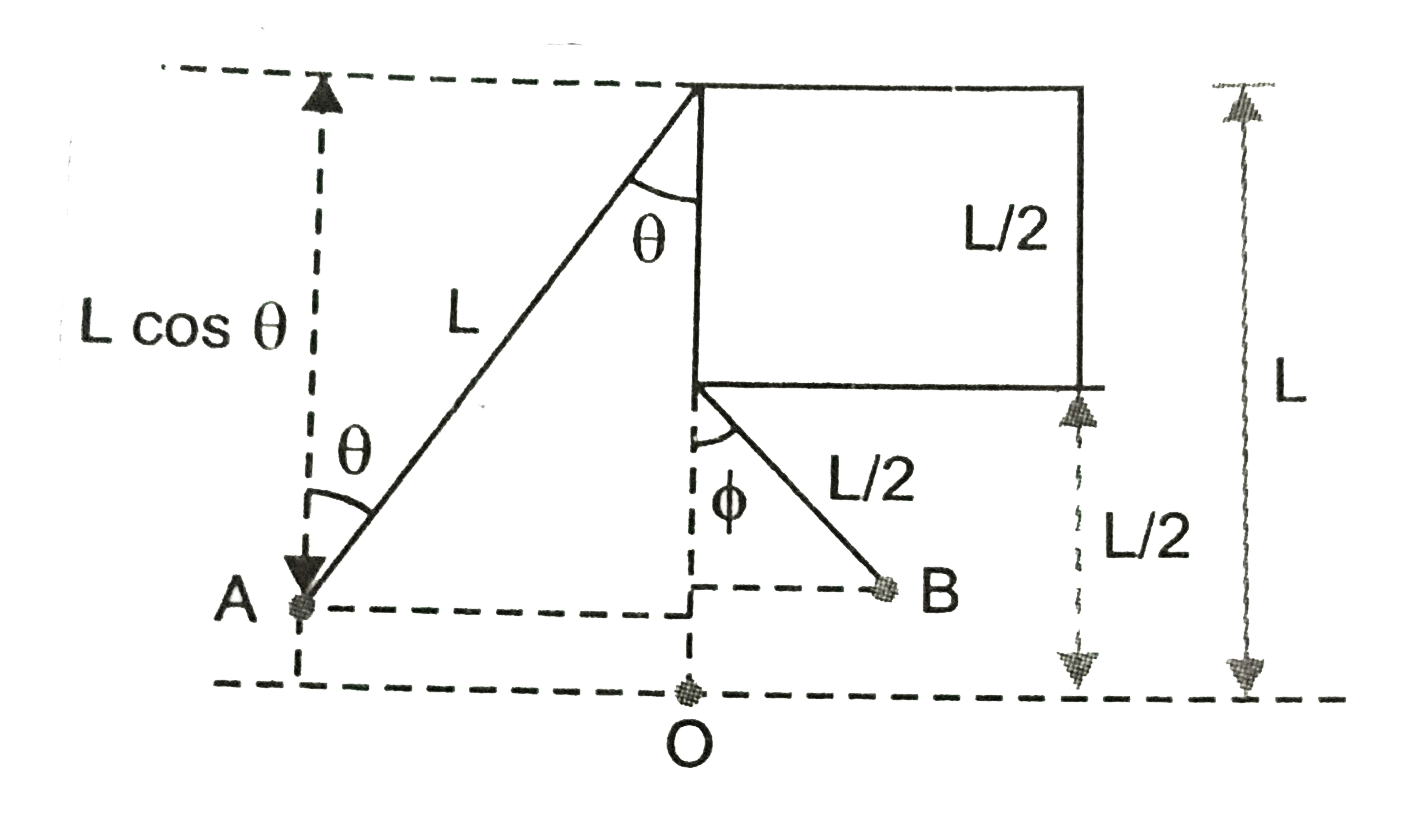
Refer to figure , At A
KE=0,PE=mg(L−Lcosθ)
=mgL(1−cosθ)
Total energy at A is
EA=0+mgL(1−cosθ)
mgL(1−cosθ)
At B, KE=0
PE=mg[L2−L2cosϕ]=(mg)L2[1−cosϕ]
Total energy at B is
EB=0+(mg)L2[1−cosϕ](mg)L2[1−cosϕ]
Accoding to law of conservation of energy
EA−EB
mgL(1−cosθ)=(mg)L2(1−cosϕ)
or 1−cosθ=1−cosϕ2
or 2−2cosθ=1−cosϕ
or 2cosθ=1+cosϕ or cosθ=1+cosϕ2
∴θ<ϕ<2θ
Hence, option (d ) is correct.
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBook:PRADEEPChapter:OSCILLATIONS AND WAVESExercise:integer type question
Explore 8 Videos
- OSCILLATIONS AND WAVESBook:PRADEEPChapter:OSCILLATIONS AND WAVESExercise:Assertion-Reason Type Questions
Explore 23 Videos
- OSCILLATIONS AND WAVESBook:PRADEEPChapter:OSCILLATIONS AND WAVESExercise:Multiple Choice Question-II
Explore 14 Videos
- MATHEMATICAL TOOLSBook:PRADEEPChapter:MATHEMATICAL TOOLSExercise:Fill in the blanks
Explore 5 Videos
- PHYSICAL WORLD AND MEASUREMENTBook:PRADEEPChapter:PHYSICAL WORLD AND MEASUREMENTExercise:Competiton Focus Jee Medical Entrance
Explore 18 Videos
Similar Questions
A simple pendulum consists of a ball of mass m connected to a string of length L. The ball is pulled aside so that the string makes an angle of 53∘ with the verticle and is released. Find the ratio of the minumum and the tension in the string.
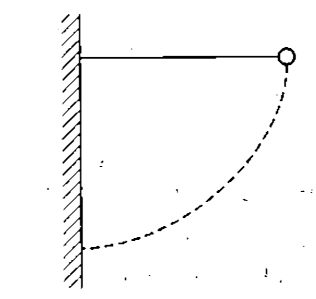
View SolutionA simple pendulum is supended from a peg on a verticl wall. The pendulum is pulled away from the wall to a horizontal position and releases as shown in figure −4.152. The ball hits the wall, the coefficient of restitution being 2/√2. What is the minimum number of collisions after which the amplitude of oscillation becomes less than 60∘
View Solution
Knowledge Check
In a simple pendulum, the breaking strength of the string is double the weight of the bob. The bob is released from rest when the string is horizontal. The string breaks when it makes an angle θ with the vertical.
Aθ=cos−1(1/3)Bθ=60∘Cθ=cos−1(2/3)Dθ=0A simple pendulum of length l and mass (bob) m is suspended vertically. The string makes an angle θ with the vertical. The restoring force acting on the pendulum is
AmgtanθB−mgsinθCmgsinθD−mgcosθA L shaped rod of mass M is free to rotate in a vertical plane about axis A A as shown in figure. Maximum angular acceleration of rod is
 A3g√10IB9g10lC9g5lD6g5√2I
A3g√10IB9g10lC9g5lD6g5√2I
A simple pendulum is released from rest with the string in horizontal position. The vertical component of the velocity of the bob becomes maximum, when the string makes an angle θ with the vertical. The angle θ is equal to
View SolutionThe mass of a simple pendulum bob is 100 gm. The length of the pendulum is 1 m. The bob is drawn aside from the equilibrium position so that the string makes an angle of 60∘ with the vertical and let go. The kinetic energy of the bob while crossing its equilibrium position will be
View SolutionA pendulum of length l=1m is released from θ0=60∘ . The rate of change of speed of the bob at θ=30∘ is.
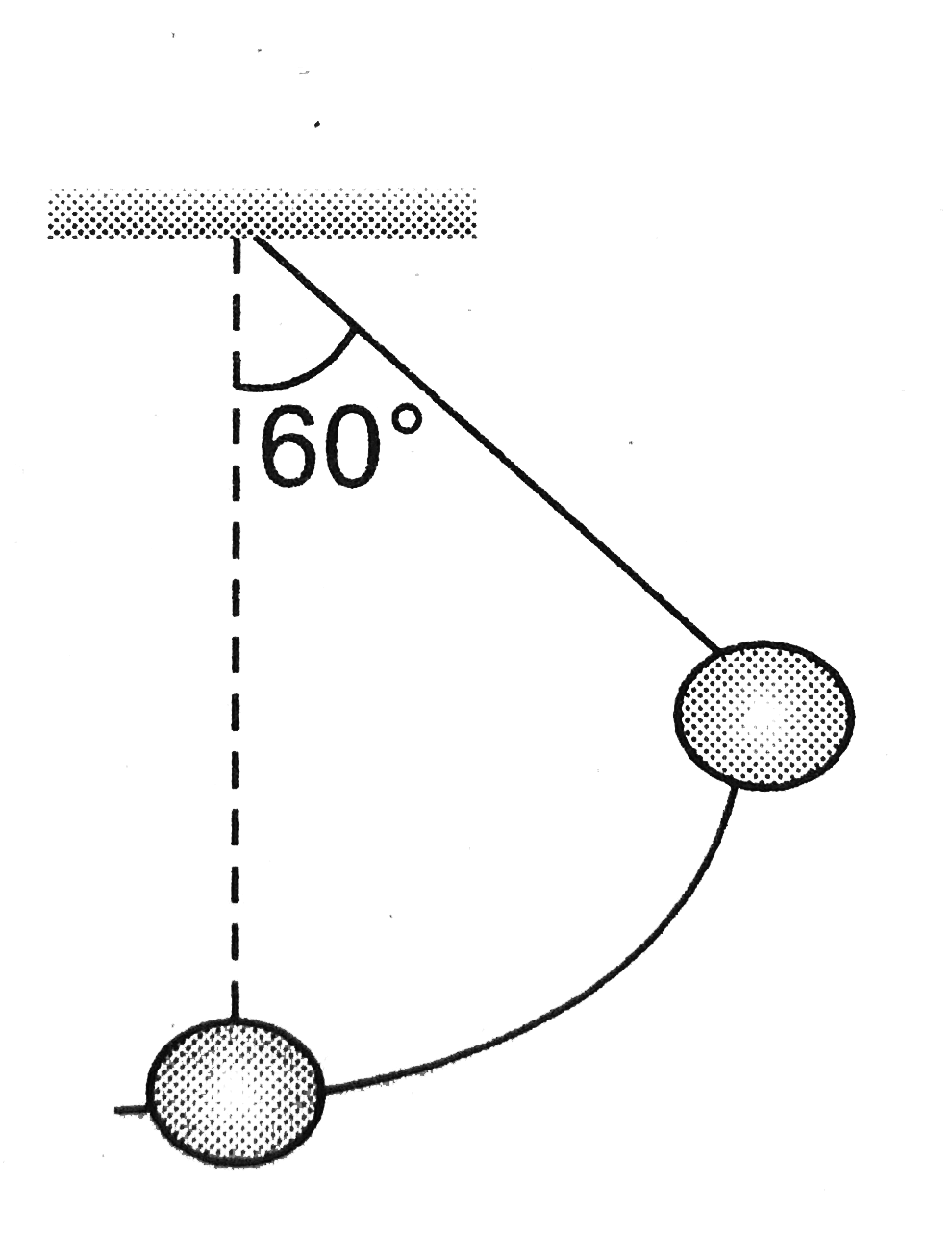
View SolutionA pendulum of length l = 1m is released from θ0=60∘. The rate of change of speed of the bob at θ=30∘ is (g=10m/s2)
View SolutionA rod of mass m and length L is hinged at its top end. If the rod is in equilibrium making an angle of 30∘ with the vertical when a horizontal force F is applied as shown in figure, then the value of F is:

View Solution

