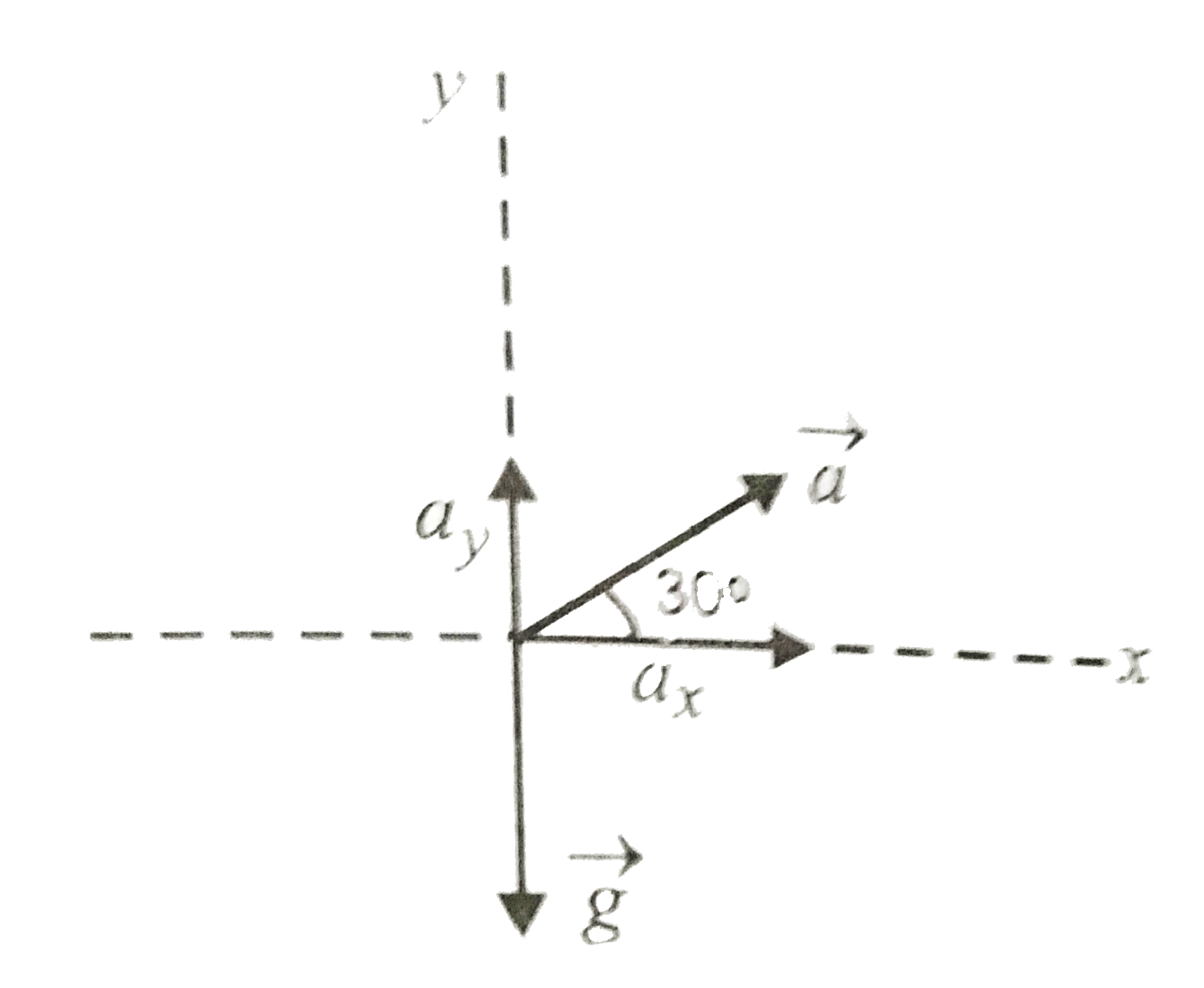
A 60cm pendulum is fixed in an aeroplane taking off at an angle $α = 30^{\circ}$ to the horizontal with an acceleration $a = 4.0 m s^{- 2}$ . Determine the period of oscillation of the pendulum.

Video Solution

Text Solution

Verified by Experts

Resolving acceleration into two rectangular components, we have
$a_{x} = a {cos 30}^{\circ} = a \frac{\sqrt{3}}{2} = 0.866 a$
$a_{6} = a sin 3 -^{\circ} = \frac{a}{2} = 0.5 a$
The aeroplane flying above can be taken as a llift moving upwards with vertical upward acceleration $a_{y} (= 0.5 a)$ . Therefore, the effective downward acceleration
$a_{y}^{'} = g + 0.5 a$
$∴$ Effective acceleration of the pendulum in aeroplane , $g^{'}$ is
${(g^{'})}^{2} = {(g + 0.5 a)}^{2} + {(0.866 a)}^{2}$
$= {(9.8 + 0.5 \times 4)}^{2} + {(0.866 \times 4)}^{2}$
$= 151.24$
or $g^{'} = 12.30 m / s^{2}$
The time period of oscillation of the simple pendulum is
$T = 2 π \sqrt{\frac{l}{g^{'}}} = 2 π \sqrt{\frac{0.6}{12.30}} = 1.388 s$

Updated on:21/07/2023

A simple pendulum $50 c m$ long is suspended from the roof of a acceleration in the horizontal direction with constant acceleration $\sqrt{3} g m / s^{- 1}$ . The period of small oscillations of the pendulum about its equilibrium position is $(g = π^{2} m / s^{2})$ ltbRgt
A $1.0 sec$
B $1.25 sec$
C $1.53 sec$
D $1.68 sec$
A seconds pendulum is suspended from the ceiling of a trolley moving horizontally with an acceleration of $4 m / s^{2}$ . Its period of oscillation is
A $1.90 s$
B $1.70 s$
C $2.30 s$
D $1.40 s$
A pendulum is suspended in a ligt and its period of oscillation when the lift is stationary is $T_{a}$ . What must be the accleraion of the lift for the period of oscillation of the pendulum to be $T_{0} / 2$ ?
A $2 g$ downward
B $2 g$ upward
C $3 g$ downward
D $3 g$ upward