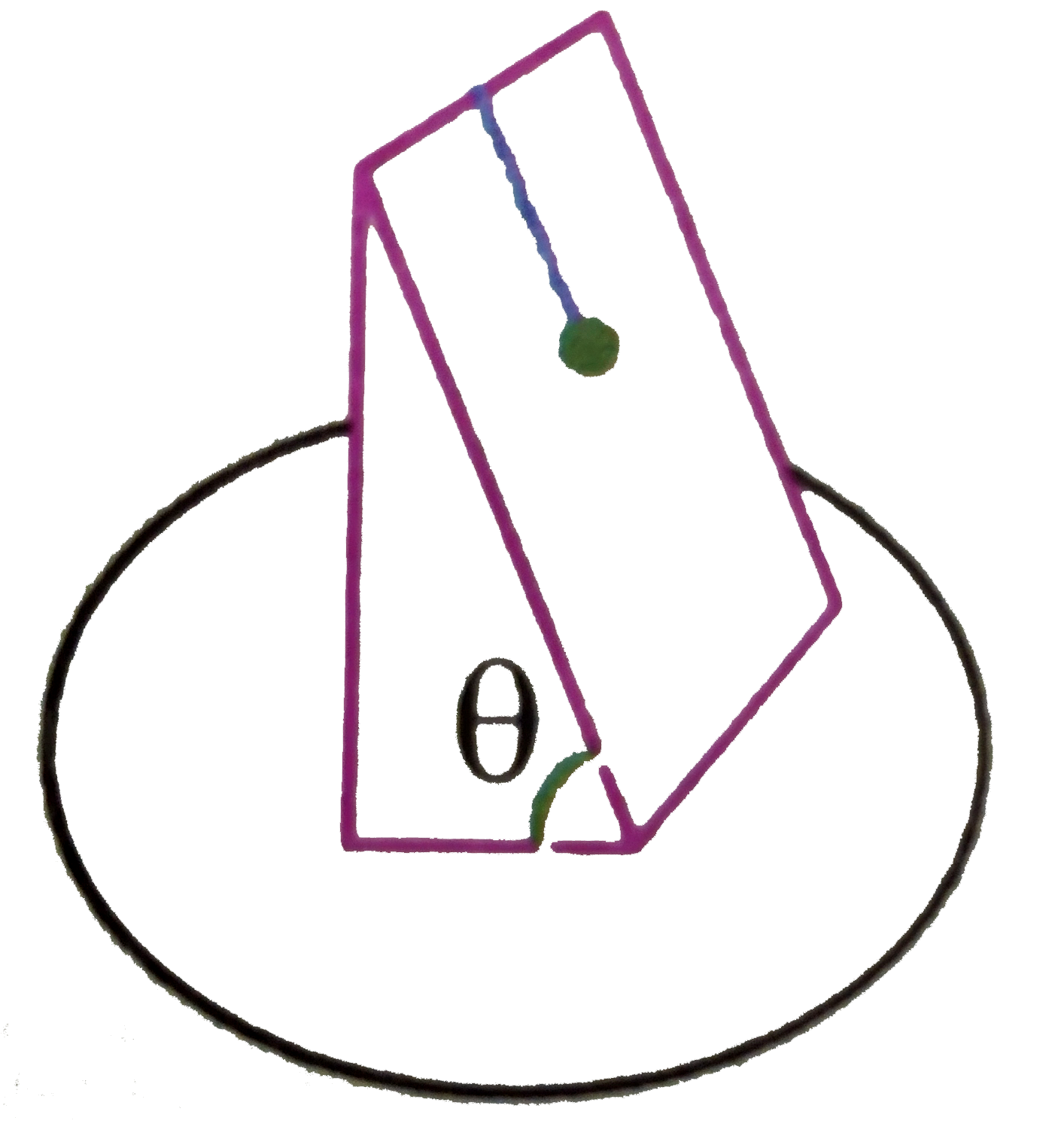
A simple pendulum is suspnded from the ceilignof a car accelerating uniformly on a horizontal road.If the acceleration is $a_{0}$ and the length of the pendulum is l, find the time period of small oscillations about the mean position.

Video Solution

Text Solution

Verified by Experts

In this problem, the pendulum has two acceleratios, a horizontal acceleration, $a_{x} = a$ and a vertical downward acceleration, $a_{y} = g$ . So, the resultant acceleration, $a = \sqrt{a x^{2} + a y^{2}} = \sqrt{a^{2} + g^{2}}$
So, the time period of oscillation of this simple pendulum is , $T = 2 π \sqrt{\frac{l}{{(a^{2} + g^{2})}^{1 / 2}}}$

|

Updated on:21/07/2023

Class 11 PHYSICS SIMPLE HARMONIC MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
A simple pendulum with a bob of mass m is suspended from the roof of a car moving with a horizontal acceleration a.
AThe string makes an angle of ${tan}^{- 1} (a / g)$ with the vertical
BThe string makes an angle of ${tan}^{- 1} (1 - \frac{a}{g})$ with the vertical
CThe tension in the string is $m \sqrt{a^{2} + g^{2}}$
DThe tension in the string is $m \sqrt{g^{2} - a^{2}}$
Question 2 - Select One
A simple pendulum $50 c m$ long is suspended from the roof of a acceleration in the horizontal direction with constant acceleration $\sqrt{3} g m / s^{- 1}$ . The period of small oscillations of the pendulum about its equilibrium position is $(g = π^{2} m / s^{2})$ ltbRgt
A $1.0 sec$
B $1.25 sec$
C $1.53 sec$
D $1.68 sec$
Question 3 - Select One
A simple pendulum of length L is suspended from the roof of a train. If the train moves in a horizontal direction with an acceleration 'a' then the period of the simple pendulum is given by
A $T = 2 π \sqrt{\frac{l}{g}}$
B $T = 2 π \sqrt{\frac{l}{g + a}}$
C $T = 2 π \sqrt{\frac{l}{(g^{2} + a^{2})}}$
D $T = 2 π \sqrt{\frac{l}{g - a}}$

PRADEEP-OSCILLATIONS AND WAVES-conceptual problems

Home
Ask Doubt
Profile