From the ceiling of a train, a pendulum of length 'l' is suspended. The train is moving with an acceleration a0 on horizontal surface. What must be the period of oscillation of pendulum?
T=2π√(lg)
T=2π ⎷(la20−g2)
T=π ⎷(la20+g2)
T=2π ⎷(la20−g2)
The correct Answer is:B
To find the period of oscillation of a pendulum suspended from the ceiling of a train that is accelerating horizontally, we can follow these steps:
Step 1: Understand the Effective Acceleration
When the train accelerates with an acceleration a0, the pendulum experiences two accelerations:
1. The gravitational acceleration g acting downwards.
2. The train's acceleration a0 acting horizontally.
Step 2: Determine the Resultant Acceleration
The effective acceleration geffective that affects the pendulum's motion can be determined using vector addition. The resultant acceleration can be calculated using the Pythagorean theorem:
geffective=√a20+g2
Step 3: Use the Formula for the Period of a Pendulum
The formula for the period T of a simple pendulum is given by:
T=2π√Lgeffective
Step 4: Substitute the Effective Acceleration
Now we can substitute the expression for geffective into the period formula:
T=2π
⎷L√a20+g2
Step 5: Simplify the Expression
We can simplify the expression further:
T=2π√L√a20+g2
Final Result
Thus, the period of oscillation of the pendulum is:
T=2π√L√a20+g2
When the train accelerates with an acceleration a0, the pendulum experiences two accelerations:
1. The gravitational acceleration g acting downwards.
2. The train's acceleration a0 acting horizontally.
The effective acceleration geffective that affects the pendulum's motion can be determined using vector addition. The resultant acceleration can be calculated using the Pythagorean theorem:
The formula for the period T of a simple pendulum is given by:
Now we can substitute the expression for geffective into the period formula:
⎷L√a20+g2
We can simplify the expression further:
Thus, the period of oscillation of the pendulum is:
Topper's Solved these Questions
Similar Questions
A simple pendulum whose length is 20 cm is suspended from the ceiling of a lift which is rising up with an acceleration of 3.0ms−2. Calculate the time-period of the pendulum.
View SolutionA bob of mass m is suspended from the ceiling of a train moving with an acceleration a as shown in figure. Find the angle θ in equilibrium position.
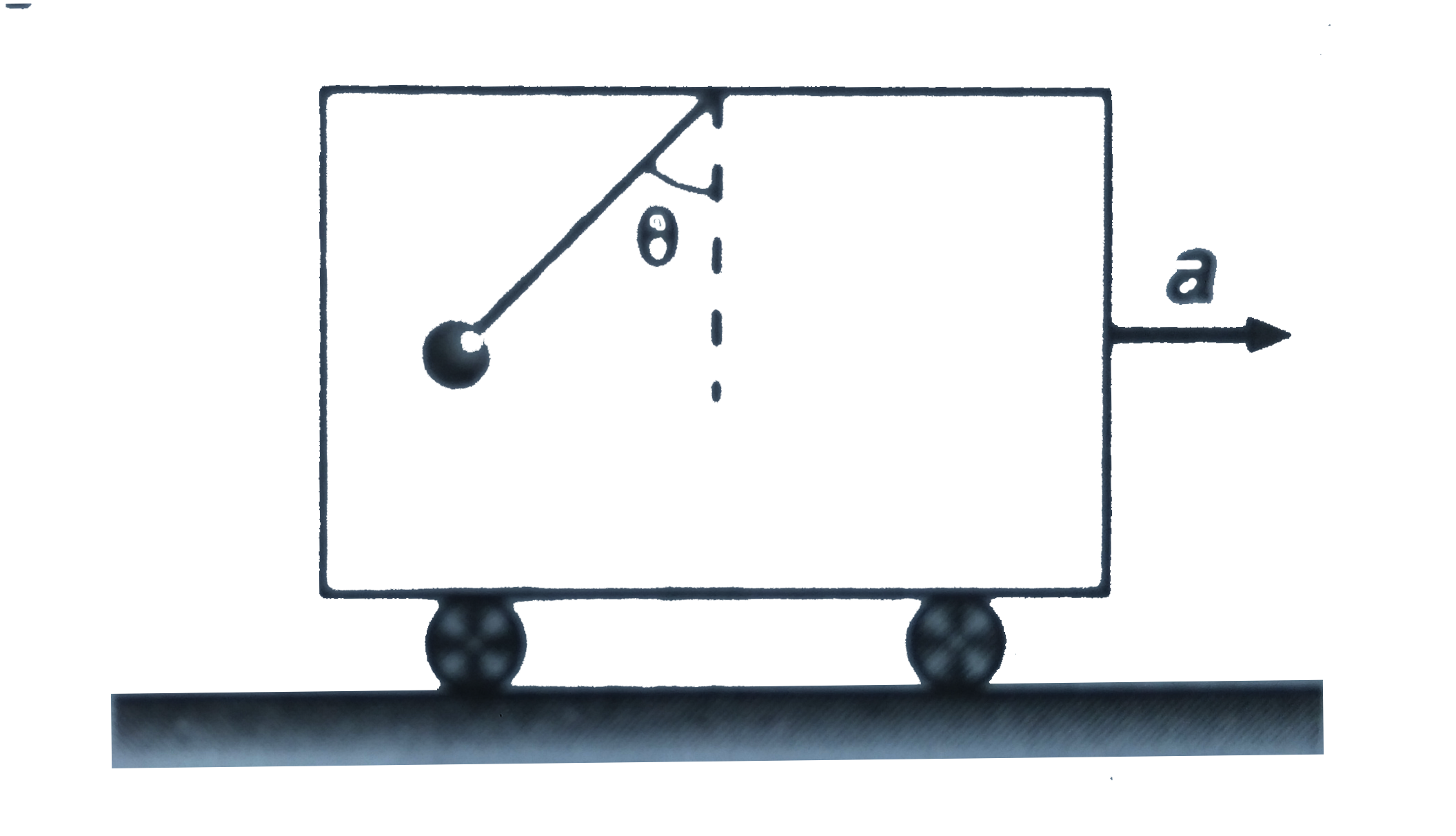
View Solution
Knowledge Check
The pendulum suspended from the ceiling of a train has a period T when the train is at rest. When the train is accelrating with a uniform acceleration, the period of oscillation will
AincreaseBdecreaseCremain unaffectedDbecome infiniteA simple pendulum of length L is suspended from the roof of a train. If the train moves in a horizontal direction with an acceleration 'a' then the period of the simple pendulum is given by
AT=2π√lgBT=2π√lg+aCT=2π√l(g2+a2)DT=2π√lg−aA seconds pendulum is suspended from the ceiling of a trolley moving horizontally with an acceleration of 4m/s2 . Its period of oscillation is
A1.90sB1.70sC2.30sD1.40s
A pendulum is suspended in a lit and its period of oscillation is T0 when the lift is stationary.
(i) What will be the period T of oscillation of pendulum, if the lift begins to accelerates downwards with an acceleration equal to 3g4 ?
(ii) What must be the accleration of the lift for the period of oscillation of the pendulum to be T02 ?
View SolutionA simple pendulum with a bob of mass m is suspended from the roof of a car moving with horizontal acceleration a
View SolutionA plumb line is suspended from a ceiling of a car moving with horizontal acceleration of a . What will be the angle of inclination with vertical
View SolutionA pendulum suspended from the ceiling of a train has time period T when the train is at rest .When the train is accelerating with a uniform acceleration ,the time period will
View SolutionAa simple pendulum is suspended from the ceiling of a vehicle which moves down an inclined plane o inclination Θ. The period of oscilation of the pendulum is
View Solution
