Two vessels have the same base area but differnent shapes. The first vessel takes twice the vloume of water that the second vessel requires to fill up to a paricular common height . Is the force exerted by water on the base of the vessel the same in the two case? If so, why do the vessels filled with water to that same height give different reading on a weighting scale ?
To solve the problem, we need to analyze the situation step by step.
Step 1: Understand the Setup
We have two vessels with the same base area but different shapes. The first vessel has a volume of water that is twice that of the second vessel when both are filled to the same height.
Step 2: Determine the Pressure at the Base
The pressure exerted by a liquid at the base of a vessel is given by the formula:
P=ρgh
where:
- P is the pressure,
- ρ is the density of the liquid (water in this case),
- g is the acceleration due to gravity,
- h is the height of the liquid column.
Since both vessels are filled to the same height h with the same liquid (water), the pressure at the base of both vessels will be the same:
P1=P2
Step 3: Calculate the Force on the Base
The force exerted by the liquid on the base of each vessel can be calculated using the formula:
F=P×A
where:
- F is the force,
- P is the pressure,
- A is the area of the base.
Since both vessels have the same base area A and the same pressure P, the force exerted on the base of both vessels will also be the same:
F1=F2
Step 4: Analyze the Weight of the Water
The weight of the water in each vessel can be calculated using the formula:
W=mg
where:
- W is the weight,
- m is the mass of the water,
- g is the acceleration due to gravity.
The mass of the water can be expressed in terms of volume and density:
m=ρV
Thus, the weight can be rewritten as:
W=ρVg
For the first vessel (volume = 2V):
W1=ρ(2V)g=2ρVg
For the second vessel (volume = V):
W2=ρVg
Step 5: Conclusion
Even though the force exerted on the base of both vessels is the same, the weights of the water in the vessels are different. The first vessel, containing twice the volume of water, will weigh twice as much as the second vessel. This difference in weight is why the vessels give different readings on a weighing scale.
Summary
- The force exerted by the water on the base of both vessels is the same because they have the same height and base area.
- The weights of the water are different due to the different volumes of water in each vessel, which is why they give different readings on a weighing scale.
We have two vessels with the same base area but different shapes. The first vessel has a volume of water that is twice that of the second vessel when both are filled to the same height.
The pressure exerted by a liquid at the base of a vessel is given by the formula:
P=ρgh
where:
- P is the pressure,
- ρ is the density of the liquid (water in this case),
- g is the acceleration due to gravity,
- h is the height of the liquid column.
P1=P2
The force exerted by the liquid on the base of each vessel can be calculated using the formula:
F=P×A
where:
- F is the force,
- P is the pressure,
- A is the area of the base.
F1=F2
The weight of the water in each vessel can be calculated using the formula:
W=mg
where:
- W is the weight,
- m is the mass of the water,
- g is the acceleration due to gravity.
m=ρV
Thus, the weight can be rewritten as:
W=ρVg
W1=ρ(2V)g=2ρVg
W2=ρVg
Even though the force exerted on the base of both vessels is the same, the weights of the water in the vessels are different. The first vessel, containing twice the volume of water, will weigh twice as much as the second vessel. This difference in weight is why the vessels give different readings on a weighing scale.
- The force exerted by the water on the base of both vessels is the same because they have the same height and base area.
- The weights of the water are different due to the different volumes of water in each vessel, which is why they give different readings on a weighing scale.
Topper's Solved these Questions
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Higher Order thinking skells
17 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Value Based Question
5 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Advanced problems for competitions
21 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance
18 Videos
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(a)
25 Videos
Similar Questions
Two vessels have the same base area but differnent shapes. The first vessel takes twice the vloume of water that the second vessel requires to fill up to a paricular common height . Is the force exerted by water on the base of the vessel the same in the two case? If so, why do the vessels filled with water to that same height give different reading on a weighting scale ?
View SolutionTwo identical cylindrical vessels have the same base area but are filled with different volumes of water . The forces on the bases of the two vessels are same .
View Solution
Knowledge Check
The height of water in a vessel is h. The vessel wall of width b is at an angle θ to the vertical. The net force exerted by the water on the wall is
 A13ρbh2gcosθB12bh2ρgC12ρbh2gsecθDZero
A13ρbh2gcosθB12bh2ρgC12ρbh2gsecθDZeroTwo vessels A and B of different shapes have the same base area and are filled with water up to the same height h (see figure). The force exerted by water on the base is FA for vessel A and FB for vessel B. The respective weights of the water filled in vessels are WA and WB. Then
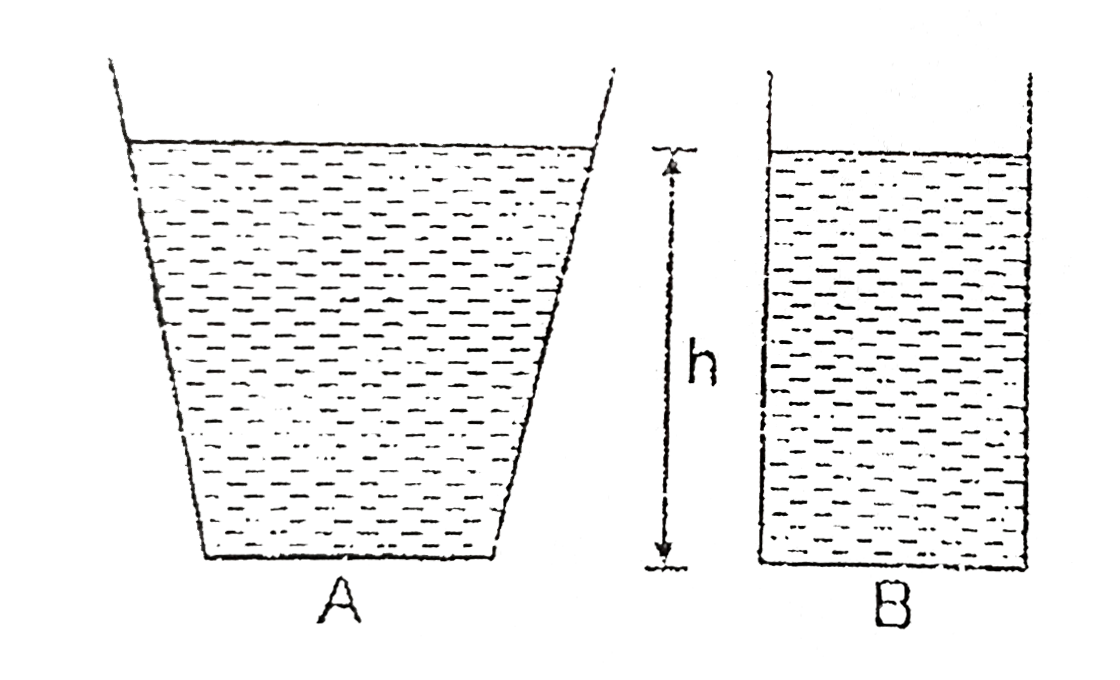 AFA>FB,WA>WBBFA=FB,WA>WBCFA=FB,WA<WBDFA>FB,WA=WB
AFA>FB,WA>WBBFA=FB,WA>WBCFA=FB,WA<WBDFA>FB,WA=WBTwo vessels A and B of different shapes have the same base area and are filled with water up to the same height h (see figure). The force exerted by water on the base is FA for vessel A and FB for vessel B. The respective weights of the water filled in vessels are WA and WB. Then
 AFA>FB,WA>WBBFA=FB,WA>WBCFA≡FB,WA<WBDFA>FB,WA=WB
AFA>FB,WA>WBBFA=FB,WA>WBCFA≡FB,WA<WBDFA>FB,WA=WB
A vessel consists of two plane mirrors at right angles (as shown in figure). The vessel is filled with water. The total deviation in incident ray is
View SolutionA vessel consists of two plane mirrors at angles (as shown in figure). The vessel is filled with water. The total deviation in incident ray is
View SolutionA vessel consists of two plane mirrors at right angles as shown in figure. The vessel is filled with water. The toal deviation in incident ray is

View SolutionTwo vessels of the same volume contain the same gas at same temperature. If the pressure in the vessels is in the ratio of 1 : 2, then
View SolutionA vessel in the form of a truncated cone has base area a1 and top area a2. It is filled to the brim with a liquid. The force at the bottom of the vessel is
View Solution
