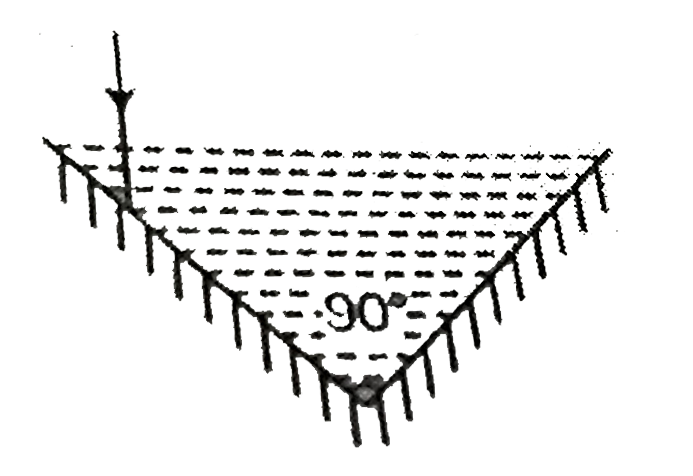
A vessel consists of two plane mirrors at right angles as shown in figure. The vessel is filled with water. The toal deviation in incident ray is
A vessel consists of two plane mirrors at right angles as shown in figure. The vessel is filled with water. The toal deviation in incident ray is

A

0∘

B

60∘

C

90∘

D

180∘

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:D

Angle between the two plance mirrors, θ=90∘
As relection is independent of medium Deviation produced by the combination of two plane mirrors is δ=2π−2θ=2π−2(π/2)=π=180∘

Updated on:21/07/2023
|
Class 12PHYSICSRAY OPTICS AND OPTICAL INSTRUMENTS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • A vessel consists of two plane mirrors at right angles (as shown in figure). The vessel is filled with water. The total deviation in incident ray is
    ocr_image

    A0∘
    B90∘
    C180∘
    DNone of the above

  • A vessel consists of two plane mirrors at angles (as shown in figure). The vessel is filled with water. The total deviation in incident ray is
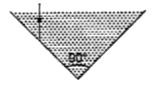    ocr_image

    A0∘
    B90∘
    C180∘
    DNone of these

  • A hollow prism is filled with water and placed in air. It will deviate the incident rays

    Atowards the base
    Baway from base
    Cparallel to base
    Dtowards or away from base depending on the location